The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).

This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.

ELECTRON CLOUDS AND PROBABlLlTY

In the attempts to refine our model of the atom, we see the division between matter and energy has become less clear.

Radiant energy is found to have many properties of particles.

Small particles of matter are found to display the characteristics of wave motion.

The purpose of this chapter is to look more closely at this wave-particle problem.

We have seen in Chapter 8 that the frequencies predicted by Bohr for the hydrogen spectrum are "essentially" correct. Note that we did not use the word "exactly."

Improved equipment has shown that the hydrogen spectrum lines predicted by Bohr are not single lines. If we were to reexamine the hydrogen spectrum with a better spectroscope, we would see that what seemed to be single lines are really several lines closely spaced.

Scientists have had to change many of their ideas about the behavior of the particles in an atom. They have done so because of the discovery of the "fine structure" of spectral lines. Bohr's use of quantum theory in the study of atomic structure has been revised to include the fine structure.

9: 1 DE BROGLIE'S HYPOTHESlS

In 1923, a French physicist, Louis de Broglie, proposed a hypothesis which led the way to the present theory of atomic structure. De Broglie knew of Planck's ideas concerning radiation being made of discrete amounts of energy called quanta. This theory seemed to give waves the properties of particles. De Broglie thought if Planck were correct, then it might be possible for particles to have some of the properties of waves.

9:2 THE APPARENT CONTRADICTiON

Waves can act as particles, and particles can act as waves. We saw how the photoelectric effect and Bohr's atom model explained light in terms of particle properties. Now let us look at a light property which can be explained by wave behavior.

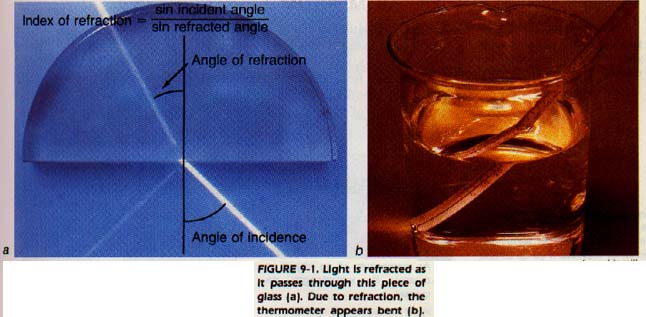
Light waves travel at different speeds in different substances. When a light wave passes from one substance into another it changes speed. If a light wave strikes a surface at an angle, it also changes direction (is bent or refracted).
The index of refraction of a substance is determined by the bending of a light wave as it passes from a vacuum into that substance. We measure the angle between the ray and the surface both before and after the ray passes through the surface.

Each substance has a characteristic index of refraction, Figure 9-1. We can identify a substance by its index of refraction. The instrument used to measure index of refraction is called a refractometer (ree frak TOM Uh tuhr).

Like light, electrons also have properties of both waves and particles. However, one cannot observe both the particle and wave properties of an electron by the same experiment.

If an experiment is done to show an electron's wave properties, the electron exhibits the properties of a wave. Another experiment, carried out to show the electron as a particle, will show that the electron exhibits the behavior of a particle.

The whole idea of the two sided nature of waves and particles is referred to as the waveparticle duality of nature.

The duality applies to all waves and all particles. Scientists are not always interested in duality. For example, when scientists study the motion of an artillery shell, wave characteristics do not enter into their study. They are only interested in the shell as a particle. However, with very small particles we cannot ignore wave properties.

For an electron, a study of its wave characteristics can tell as much about its behavior as a study of its particle characteristics.

9:3 MOMENTUM

The product of the mass and velocity of an object is called the momentum of the object. In equation form, mv = p where m is the mass, v is the velocity, and p is the symbol for momentum. You should note that velocity includes not only the speed but also the direction of motion. Recall de Broglie's equation for the wavelength of the wave associated with a particle in motion.

An object may have a large momentum because of a large mass or a large velocity. In either case, it would have a small wavelength. Therefore, the wave properties of all objects in motion are not always of interest to the scientist.

There is a basic difference between Newtonian and quantum mechanics. Newtonian mechanics describes the behavior of visible objects traveling at ordinary velocities. Quantum mechanics describes the behavior of extremely small particles traveling at velocities near that of light.

To the chemist, the behavior of the electrons in an atom is of greatest interest. To be able to give a full description of an electron, we must know two things: where it is, and where it is going. In other words, we must know the electron's present position and its momentum.

From the velocity and position of an electron at one time, we can calculate where the electron will be some time later.

9:4 MEASURlNG POSlTlON AND MOMENTUM

Werner Heisenberg further improved the ideas about atomic structure. He pointed out that it is impossible to know both the exact position and the exact momentum of an object at the same time. Ah, the Uncertainty Principle.

Let us take a closer look at Heisenberg's ideas. To locate the exact position of an electron, we must be able to "look" at it. When we look at an object large enough to see with our eyes, we actually see the light waves which the object has reflected

When radar detects an object, the radar receiver is actually "seeing" the radar waves reflected by the object. In other words, for us to see an object, it must be hit by some kind of radiant energy.

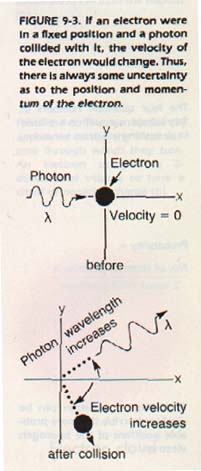
However, a collision between a photon and an electron results in a large change in the energy of the electron. Let us assume we have "seen" an electron, using some sort of radiant energy as "illumination."

We have found the exact position of the electron. However, we would have little idea of the electron's velocity. The collision between it and the photons used to see it has caused its velocity to change. Thus, we would know the position of the electron, but not its velocity. On the other hand, if we measure an electron's velocity, we will change the electron's position.

We would know the velocity fairly well, but not the position. Heisenberg stated that there is always some uncertainty as to the position and momentum of an electron. This statement is known as Heisenberg's uncertainty principle.

The uncertainty of the position and the uncertainty of the momentum of an electron are related by Planck's constant.

Thus, since h is constant, the more certain we are of the position of the electron, the less certain we are of its momentum. The more certain we are of its momentum, the less certain we are of its position. Whew!

9:5 SCHRODINGER'S WORK

Chemists and physicists now found themselves unable describe the exact structure of the atom. Heisenberg had, in effect stated that the exact motion of an electron was unknown and could never be determined. Notice, however, that Heisenberg's principle of uncertainty treats the electron as a particle. What happens if the electron is treated as a wave? The wave nature of the electron was investigated by the Austrian physicist, Erwin Shrodinger.

Schrodinger treated the electron as a wave and developed a mathematical equation to describe its wave-like behavior. Schrodinger's equation related the amplitude of the electron wave ,psi, to any point in space around the nucleus.

He pointed out that there is no physical meaning to the values of psi. You should avoid trying to assume one. Terms for the total energy and for the potential energy of the electron are also part of this equation.

In computing the total energy and the potential energy, certain numbers must be used. For example, the term for the total energy is:

9:6 WAVE-MECHANICAL VlEW OF THE HYDROGEN ATOM

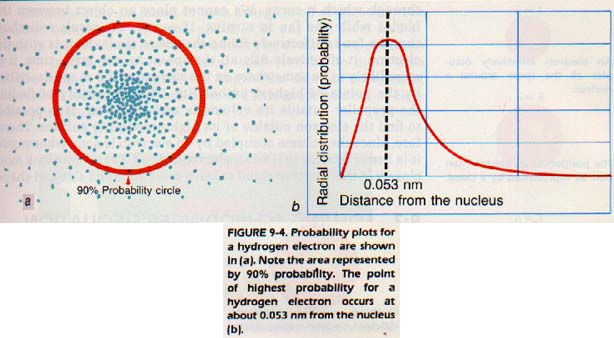
Schrodinger's wave equation is used to determine the probability of finding the hydrogen electron in any given place. The probabilities can be computed for finding the electron at different points along a given line away from the nucleus. One point will have a higher probability than any other, Figure 9-4. To carry the process even further, the probabilities for thousands of points in space may be calculated.

There will be many points of equal probability. If all the points of highest probability are connected, some three dimensional shape is formed. These shapes will be shown later in the chapter.

The most probable place to find the electron will be some place on the surface of this calculated shape. Remember that this shape is only a "mental model" and does not actually exist. It is something we use in our minds to help locate the electron.

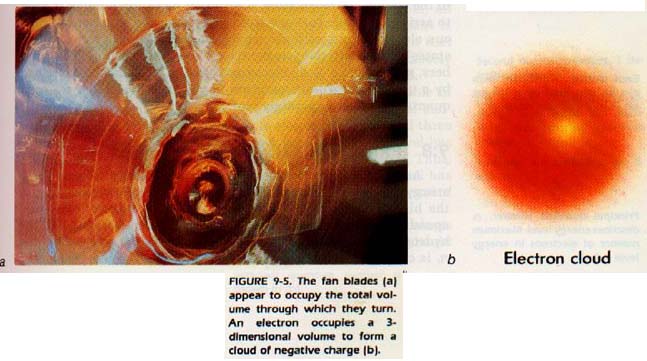
There is another way of looking at probability. The electron moves about the nucleus in such a way as to pass through the points of high probability more often than through any other points. The electron is traveling at a high rate of speed. If the electron were visible to the eye, its rapid motion would cause it to appear as a cloud.

Think of a fan as shown in Figure 9-5. When the fan is tuning, it appears to fill the complete circle through which it turns. We cannot place an object between the blades while the fan is turning. If we do, the result will show that the fan is effectively filling the entire circle.

So it is with the electron. It effectively fills all the space. At any given time, it is more likely to be somewhere on the surface of the shape described by the points of highest probability.

The probability of finding the propeller outside its volume is zero. However, it is possible to find the electron outside of its high probability surface. Therefore, since the volume occupied by an electron is somewhat vague, it is better to refer to it as an electron cloud. Let us now look more closely at this electron cloud to learn more about its size and shape.

9:7 SOLVING SCHRODINGER'S EQUATlON

Solutions to the Schrodinger equation proved difficult for even the best mathematicians. It has been solved exactly only for simple cases involving the hydrogen atom. The use of quantum numbers in the solution of the wave equation was mentioned in Section 9:5.

These numbers represent different energy states of the electron. In Schrodinger's atomic model, changes between energy states must take place by emission or absorption of whole numbers of photons.

For the simple hydrogen atom, solution of the wave equation gives us accurate energy states. The differences between these energy states correspond to the lines observed in the hydrogen spectrum.

With more complex atoms, however, the interaction of electrons makes solution of the equation impossible. Recall that electrons all have the same charge which causes them to repel each other. In spite of this difficulty, scientists can come close to finding the electronic structure of atoms by making an assumption.

They first calculate the various single energy states in the simple hydrogen atom. A different quantum number is used to arrive at a value for each state. They then assume that the various electrons in a multielectron atom occupy these same energy states without affecting each other.

There are four quantum numbers, n, 1, m, and s.

Each electron within an atom can be described by a unique set of four quantum numbers.

We will discuss each quantum number separately starting with n.

An electron effectively occupies all the space around a nucleus.

9:8 PRlNClPAL QUANTUM NUMBER

An electron can occupy only specific energy levels. These energy levels are numbered, starting with 1 and proceeding to the higher integers. The principal quantum number (n) corresponds to the energy levels (1, 2, 3,... n) calculated for the hydrogen atom.

The number of the energy level, referred to as n, is called the principal quantum number.

Electrons may be found in each energy level of an atom. The greatest number of electrons possible in any one level is 2n². Thus, in the first level (n = 1), there may be at most two electrons (2 x 1²). In the fourth energy level, there can be no more than 32 electrons (2 x 4²). Figure 9-6 shows the relative energies of the various levels. It also indicates the maximum number of electrons possible in each level.

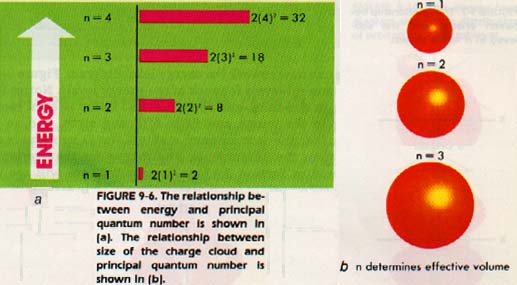
9:9 ENERGY SUBLEVELS

The second quantum number is 1. In a hydrogen atom, all electrons in one level have the same energy. This statement is not true for any other atom. Spectrum studies have shown that an energy level is actually made of many energy states closely grouped together.

We can refer to these states as sublevels. Each level has a number of sublevels equal to the value of the principal quantum number. You can expect to find one sublevel in the first level, two sublevels in the second level, and three sublevels in the third level.

The lowest sublevel in each level has been named s; the second, p; the third, d; and the fourth, f.

Thus, the first level has only an s sublevel. The second energy level has s and p sublevels, while the third energy level has s, p, and d sublevels.

As an example, consider the n = 4 level. Instead of the single energy line as was shown in Figure 9-6, the n = 4 level should look as shown in Figure 9-7 with all sublevels shown.

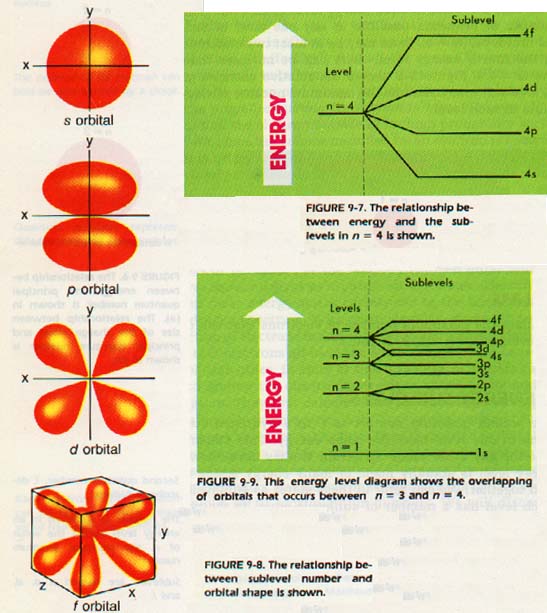
We can now rework the energy level diagram. Figure 9-9 shows the various sublevels for each of the energy levels. Notice the overlapping in the third and fourth levels.

There is even more overlapping in the fourth and fifth, fifth and sixth, and so on. The effect is that the atom is more stable if the 4s sublevel is of lower energy than the 3d sublevel. The reason for the overlap will be considered in Section 9:11. In Section 9:l2 we will see why the overlap is important in understanding atomic structure.

9: 10 ORBlTALS

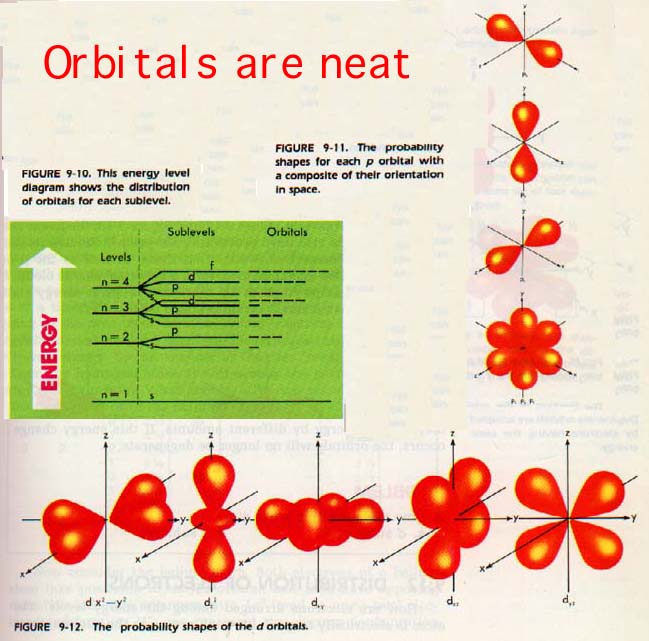
The third quantum number is m. Calculation has shown that any s sublevel may contain one pair of electrons; any p sublevel, three pairs; and d sublevel, five pairs; and any f sublevel, seven pairs.

Each pair in a given sublevel has a different place in space. This space occupied by one pair of electrons is called an orbital. We can now redraw the energy level diagram with the orbitals shown. Each short line in Figure 9-10 represents an orbital that can hold a pair of electrons.

9:11 SHAPE OF THE CHARGE CLOUD

We now want to see how these various energy levels and sublevels affect the electron charge cloud described in Section 9:6. In general, the size of the charge cloud is related to n, the principal quantum number.

The larger the value of n, the larger the cloud. However, there are also other factors which govern the size of the cloud.

Electrons are repelled by each other; they are also attracted by the positively charged nucleus. At the same time, other electrons serve to screen the effect of the nucleus.

Picture an electron A between the nucleus and electron B. Electron A reduces the attraction of the nucleus for electron B. Thus, the size of the charge cloud is not controlled by any single factor.

The sum of all electron clouds in any sublevel (or energy level) is a spherical cloud. However, orbitals have characteristic probability shapes of their own. For example, look at Figure 9-11 (above). The three p orbitals can be directed along the three mutually perpendicular x, y, and z axes. They are sometimes labeled as p_x, p_y, and p_z.

As shown in Figure 9-12 (above) and Figure 9-13 (below), the five d and seven f orbitals also have probability shapes which have relationships among themselves.

Notice that these, as well as the p orbitals, when filled and combined, form a spherical charge cloud. A large, simple shape (such as 4s) represents a lower energy state in an atom than a small, complex shape (such as 3d).

The third quantum number, m, defines each orbital more precisely by indicating its direction in space. There are three possible values for m when discussing a p sublevel.

The numbers designate orbitals aligned along the x, y, and z axes.

There are five values for m in a d sublevel and seven values for m in an f sublevel.

Orbitals which are alike in size and shape and differ only in direction have the same energy. Orbitals of the same energy are said to be degenerate. When atoms react, degenerate orbitals may change energy by different amounts. If this energy change occurs, the orbitals will no longer be degenerate.

9:12 DlSTRlBUTlON OF ELECTRONS

How are electrons arranged among the energy levels? The atom is electrically neutral. For each proton in the nucleus, there is one electron in the charge cloud. Thus, as the atomic number increases, the number of electrons increases.

The energy levels in an atom can be thought of as a rooming house in which the choice of double rooms are on the ground level. Electrons, as tenants, will tend to fill the better (lower) rooms first, one at a time.

Then, they double up in these better rooms before going to the next level. In other words, electrons occupy the energy level and sublevel that produces the arrangement with the lowest energy.

Let us consider as the first "tenant," the electron from the hydrogen atom. It will occupy the position of least energy, the 1s orbital. What about a different set of room tenants, the two electrons of the helium atom?

Before we can answer this question, we must consider a principle which helps to explain the arrangement of electrons. It has been found that no two electrons in an atom have the same set of quantum numbers. This behavior was first observed and stated by Wolfgang Pauli and is called the Pauli Exclusion Principle. The quantum numbers n, 1, and m describe relative cloud size (n), shape of the cloud (1), and direction of the cloud (m).

The fourth quantum number, s, describes the spin of the electron, clockwise or counterclockwise. If two electrons occupy the same orbital, they have opposite spins. Otherwise their quantum numbers would be identical, Figure 9-14.

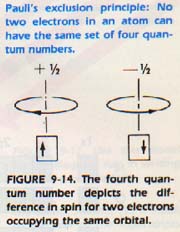
Now consider the helium atom. Both electrons of a helium atom take positions in the Is orbital, and thus have opposing spins. We call this arrangement a ls² (read as one-s-two) electron configuration.

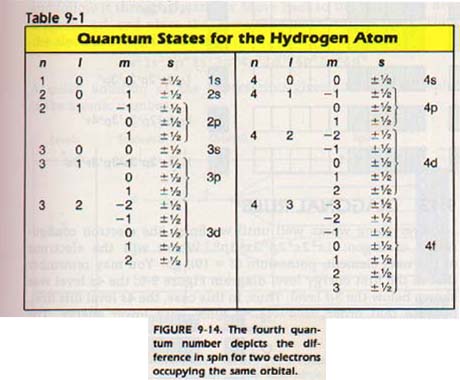
We can represent the electron configuration by a diagram like that in Figure 9-15. In the diagram, each box stands for an orbital. Arrows are used to indicate the direction of the spin of the electrons in the orbital.

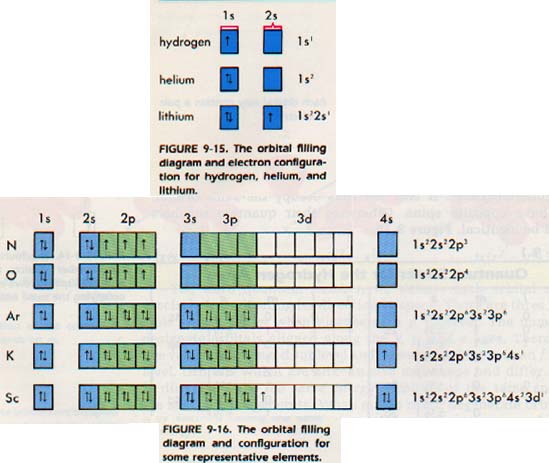
The electron configuration of lithium (Z = 3) shows both positions in the Is orbital and one position in the 2s orbital filled. We designate this arrangement as ls²2s^l, Figure 9-15.

Let's move on to the nitrogen atom and see how the seven electrons are distributed. We would expect two electrons in the Is orbital, two in the 2s, and three in the 2p. This arrangement can be indicated as in Figure 9-16 (above), where each arrow represents an electron.

The opposing arrows indicate opposite spins. Notice that, each electron takes an empty orbital within a sublevel, if possible, rather than pair with another. This arrangement is reasonable because the negative electrons repel each other.

It requires no more energy since all orbitals in a sublevel of an atom are degenerate. Since each orbital has a different orientation in space, electrons in different orbitals are farther apart than electrons in the same orbital. The electrons in the oxygen atom are arranged as shown in Figure 9-16 (above). The eighth electron enters the partially filled 2p orbital.

9.13 DlAGONAL RULE

Everything works well until we finish the electron configuration of argon: ls²2s²2p⁶3s²3p⁶.

Where will the electrons of the next element, potassium (Z = 19), go?

You may remember that in the first energy level diagram Figure 9-9, the 4s level was shown below the 3d level. Thus, in this case, the 4s level fills first, because that order produces an atom with lower energy.

The potassium configuration, therefore, is ls²2s²2p⁶3s²3p⁶4s¹. Calcium (Z = 20) has the configuration ls²2s²2p⁶3s²3p⁶4s². Scandium, however, begins filling the 3d orbitals, and has a configuration of ls² 2s² 2p⁶3s² 3p⁶4s² 3d^l.

In many atoms with higher atomic numbers, the sublevels ere not regularly filled. It is of little value to memorize each configuration. However, there is a rule of thumb which will give a correct configuration for most atoms in the ground state. It is a thumb rule because we make an assumption that is not always true.

The order of increasing energy sublevels is figured for the one-electron hydrogen atom. In a multielectron atom, each electron affects the energy of the others. Consequently, there are a number of exceptions to the rule of thumb.

We will explore these exceptions more fully in the next chapter. This rule of thumb is called the diagonal rule and is shown in Figure 9-17. If you follow the diagonals, listing the orbitals passed, you can find the electron configuration of most atoms.

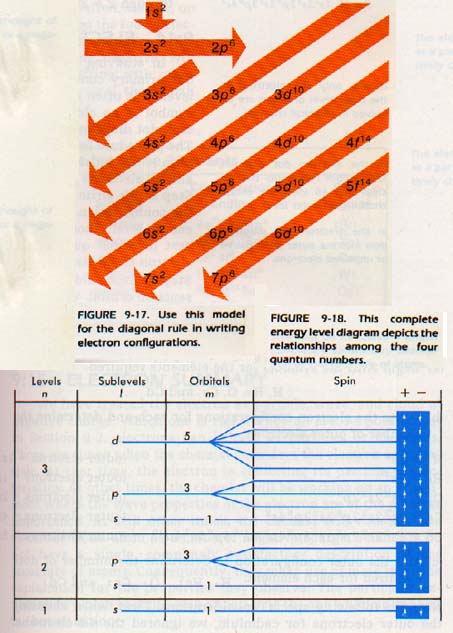
As an example, suppose you are to find the electron configuration of zirconium (Z = 40). Begin with the Is level, drop to the 2s and move over to the 2p. Follow the diagonal to 3s and move to 3p. Follow the diagonally 4s. Move back up to the tail of the next diagonal at 3d and follow it through 4p and 5s. Move back to the tail of the next diagonal 4d, and place the remaining two electrons there. Thus, the electron configuration is

A quick addition of the superscripts gives a total of 40, which is the atomic number.

9:14 ELECTRON DOT DlAGRAMS

In studying electrons in atoms in the following chapters, our primary concern will be the electrons in the outer energy level. It is often useful to draw these outer electrons around the symbol of an element. This notation is referred to as an electron dot diagram.

The procedure for drawing electron dot diagrams follows.

Step 1. We let the symbol of the element represent the nucleus and all electrons except those in the outer level.

Step 2. We write the electron configuration of the element. From the configuration we select the electrons which are in the outer energy level. Those in the outer level are the ones with the largest principal quantum number. Remember that n represents electron cloud size.

Step 3. Each "side" (top, bottom, left, right) of the symbol represents an orbital. We draw dots on the appropriate "sides" to represent the electrons in that orbital. It is important to remember which electrons are paired and which are not. It is not important which side represents which orbital.

9: 15 ELECTRON SUMMARY

We have treated the electron as particle, wave, and cloud of negative charge. Which one is right? They all are. As pointed out in Section 9-2, electrons can behave as particles or as waves.

There are times when the chemist considers the electron as a particle. At that time, the electron is exhibiting its particle characteristics. At other times, the chemist will be working on an experiment where the wave properties of the electron are of the greatest importance. At still other times, the chemist will consider the electrons in an atom as a cloud of negative charge.

Scientists do not have a single, completely satisfactory description of the structure of atoms. Consequently, they make use of more than one explanation for the properties they observe. The particular explanation which best fits each situation is the one which is applied in that situation.

1. De Broglie first pointed out the wave-particle duality of nature. His idea
was that all particles exhibit some wave characteristics, and vice versa. 9:1

2. The momentum of an object is the product of its mass and velocity. Wavelength varies inversely as momentum. 9:3

3. Heisenberg's uncertainty principle concerns the process of observing an electron's position or its velocity. It is impossible to know accurately both the position and the momentum of an electron at the same time. 9:4

4. Schrodinger developed a mathematical equation which describes the behavior of the electron as a wave. The solution set of the wave equation can be used to calculate the probability of finding an electron at a particular point.:

5. Because of the electron's high velocity, it effectively occupies all volume defined by the path through which it moves. This volume called the electron cloud. 9:6

6. The principal quantum number (n = 1, 2, 3,..) is the number of energy level and describes the relative electron cloud size. 9:8

7. Each energy level has as many sublevels as the principal quantum number. The second quantum number (1 = s, p, d, f...) describes the of the cloud. 9:9

8. The third quantum number, m, describes the orientation in space of orbital. 9:10, 9

9. The fourth quantum number, s, describes the spin direction of an electron.

10. Each orbital may contain a maximum of one pair of electrons. Electrons in the same orbital have opposite spins. s:12

11. Pauli's exclusion principle states that no two electrons in an atom have the same set of quantum numbers. 9:12

12. Electrons occupy first the empty orbital giving the atom the lowest energy. s:12

13. The diagonal rule can be used to provide the correct electron configuration for most atoms.

14. The chemist is primarily concerned with the electrons in the outer energy level. Electron dot diagrams are useful in representing the outer level electrons. s:14

Return to the Textbook Menu

Go to Textbook Assignments:

Return to the Big Chem Page