The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).

This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.

Thus far, we have discussed two properties of matter: inertia and energy. We refer to properties as we describe materials. Thus, it is helpful to learn how to measure properties of matter.

In order to make a measurement, we must meet three basic requirements.:

1. We must know exactly what we are trying to measure.

2. We must have some standard with which to compare whatever we are measuring.

3. We must have some method of making this comparison.

When we describe a property in words, we are characterizing the object qualitatively. When the property can be measured and described by a number of standard units, we have characterized the object quantitatively.

2:1 THE lNTERNATlONAL SYSTEM (S1)

The standard units of measurement in science are part of a measuring system called the International System (SI). The letters are reversed in the symbol for the system because they are taken from the French name Le Systme International d' Unites. SI is used by all scientists throughout the world and is used in everyday life in almost all countries. SI is a modern version of an older system called the metric system.

Most countries have converted or are in the process of converting to SI. This measurement system will be used throughout the text. One important feature of SI is its simplicity. Seven basic Units are the foundation of the International System. These units are shown in Table 2-1.

Detailed definitions of these units are found in Table A-l of the Appendix. We will discuss length, mass, time, and temperature in this chapter. Amount of substance will be discussed in Chapter 5 and electric current in Chapter 27. Luminous intensity will not be used in this book. The seven base units are shown so you can see the simplicity of SI.

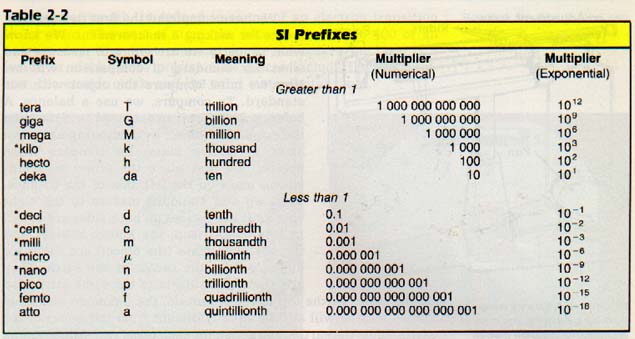
In SI, prefixes are used to obtain different units for measuring the same property. SI prefixes and their equivalents are listed in Table 2-2.

2:2 MASS

In chemistry, finding the amount of matter is very important. For instance, we may wish to measure the amount of wood in a small block. One way of measuring is to weigh the block.

Suppose we weigh such a block on a spring scale and find that its weight is one newton, (N). An apple weighs about 1 N.

Now suppose we take the scale and the block to the top of a high mountain. There we weigh the block again. The weight now will be slightly less than one newton. The weight has changed because the weight of an object depends on its distance from the center of the earth.

Weight is a measure of the force of gravity between two objects. For our purposes, these two objects are the block and the earth. This force of gravity changes when the distance from the center of the earth changes. We have seen that the weight of an object can vary from place to place. In scientific work, we need a measurement which does not change from place to place.

This measurement is called mass. Mass is a measure of the quantity of matter.

The standard for mass is a piece of metal kept at the International Bureau of Weights and Measures in Svres, France. This object is called the International Prototype Kilogram. Its mass is defined as one kilogram (kg).

The Boom's mass is 80 kg. His weight is 784 N. A kilogram has a weight of 9.8 N at sea level.

We have completed the first two requirements for making a measurement. We know what property we are going to measure and what our standard of comparison will be. Now we must compare the object with our standard. To compare, we use a balance.

A balance is an instrument used to determine the mass of an object by comparing unknown mass to known mass. To compare these masses, we first place the object with unknown mass on the left side of the balance. Then we add standard masses to the right side until the masses on both sides are equal.

In this comparison, the known masses and the unknown mass (the object) are the same distance from the center of the earth. They are, therefore, subject to the same attraction by the earth.

At the top of the mountain, the unknown mass and known masses will still be equally distant from the center of the earth. Thus, the earth's attraction for each mass will still be equal, the mass of the object as compared to the standard will be the same.

The balance will indicate no change in mass. The process of measuring mass by comparing masses on a balance is called massing.

Unfortunately, many terms which apply to the measurement of weight are often incorrectly applied to the measurement of mass. For example, standard masses used on the balance are often incorrectly called "weights."

Also, the process of using a balance to compare masses is often incorrectly called "weighing." The SI standard of mass is the kilogram (kg). However, the kilogram is too large a unit for everyday use in the chemical laboratory. For this reason, the gram (g), one-thousandth of a kilogram, is commonly used.

2:3 LENGTH

A second important measurement is that of length. Length is the distance covered by a line segment connecting two points. The standard for measuring length is defined in terms of the wavelength of a particular color of light (Table A-l of the Appendix), The standard unit of length is the meter (m). Length is usually measured with a ruler or similar device.

2:4 TlME

A third basic measurement is time. Time is the interval between two occurrences. Our present standard of time, like our standard of length, is defined in terms of an electron transition in an atom. The unit of time, the second (s), is 1/86 400 of an average day.

The most common device for measuring time is a watch or clock. More precise time pieces include the chronometer, the atomic clock, and the solid state digital timer.

2:5 TEMPERATURE

"What a hot day it is" What does this expression mean? It means that the heat content per unit volume of air that day is greater than usual. What is heat? Heat is a form of energy. Heat always flows from a region of higher intensity to one of lower intensity. Temperature is a measure of heat intensity. Heat flows until the heat intensity (temperature) is the same everywhere. If one end of a metal rod is heated, the other end eventually becomes warm.

A thermometer is the most common instrument used to measure temperature. When the bulb is heated, the mercury expands and rises in the tube. When the bulb is cooled, the mercury contracts and the height of the mercury column decreases.

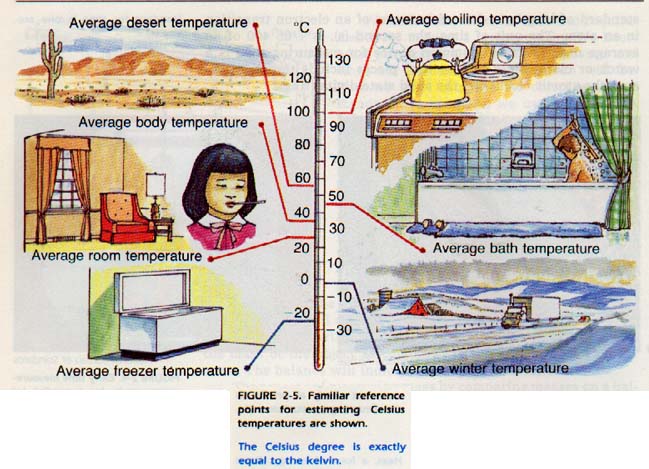
The height of the mercury column can thus be used to measure temperature. The temperature can be read directly from the scale on the tube. The unit of temperature is the kelvin (K).

We will not define this unit until Chapter 15. However, the kelvin has a direct connection with a more familiar unit, the Celsius degree (C^o). The Celsius temperature scale is based on the fact that the freezing and boiling temperatures of pure water under normal atmospheric pressure are constant. The difference between the boiling and freezing points is divided into 100 equal intervals.

Each interval is called a Celsius degree. The point at which water freezes is labeled zero degrees Celsius (O^oC). The point at which water boils is labeled 100^oC. The Celsius degree is exactly equal to the kelvin. We will use both units in our study of chemistry.

2:6 DERlVED UNlTS

By combining the fundamental SI units, we obtain measurement units used to express other quantities. Distance divided by time equals speed. If we multiply length by length, we get area. Area multiplied by length produces volume. The SI unit of volume is the cubic meter (m³). However, this quantity is too large to be practical for the laboratory. Chemists often use cubic decimeters (dm3) as the unit of volume. One cubic decimeter is given another name, the liter (L). The liter is a unit of volume. One liter equals 1OOO milliliters (mL) and 1OOO cubic centimeters (cm³).

From these facts, you can see that

The units used to express measurements of speed, area, and volume are called derived units. You saw that area and volume measurements are expressed using length units. The units used to express speed, such as kilometers per hour or meters per second, combine fundamental units of length and time.

2:7 SlGNlFlCANT DIGITS

Suppose we want to measure the length of a strip of metal. We have two rulers. One ruler is graduated in centimeters. The other is graduated in millimeters. With which ruler can we obtain a better measurement of length? The length of the strip measured in millimeters is the more significant measurement since it is closer to the actual length of the strip. We say that the measurement in millimeters has more significant digits than the measurement in centimeters.

The measurement of the centimeter scale lies approximately 6/lO of the way from the 13-cm mark to the l4-cm mark. This length is recorded as 13.6 cm.

On the millimeter ruler, the length lies approximately 3/10 of the way from the l3.6-cm mark to the l3.6-cm mark. This length is recorded as l3.63 cm. The measurement 13.6 cm has three significant digits. The measurement l3.63 cm has four significant digits. The last digit is uncertain (an estimate).

The exactness of measurements is an important part of experimentation. The exactness of a measurement is indicated by the number of significant digits in that measurement.

The observer and anyone reading the results of an experiment wants to know the number of significant digits in any observation.

The following rules are used to determine the "Number of significant digits" in a recorded measurement:

1. Digits other than zero are always significant.

2. Any final zero or zeros used after the decimal point are significant.

3. Zeros between two other significant digits are always significant.

4. Zeros used solely for spacing the decimal point are not significant.

The zeros are placeholders only.

2:8 ACCURACY AND PREClSlON

The terms accuracy and precision are often used in discussing measurements. Accuracy refers to quality of the measuring instrument as compared with the standard for that measurement.

A micrometer used to measure engine parts may approximate the standard very closely. The micrometer has a high degree of accuracy. A plastic ruler has a low degree of accuracy.

Precision refers to uncertainty in measurement.

A reflection of uncertainty is the relative error. Relative error is often expressed as the percentage uncertainty in the measurement.

2:9 HANDLlNG NUMBERS IN SClENCE

In this course we will sometimes use very large numbers. For example, Avogadro's number is 602 217 000 000 000 000 000.

We will also use very small numbers. The distance between particles in a salt crystal is 0.000 000 002 814 cm.

In working such numbers it is easy to drop a zero or to lose a decimal. Scientific notation makes it easier to work with very large or small numbers. In scientific notation, all numbers are as the product of a number between 1 and 10 and a whole-number power of 10.

One advantage of scientific notation is that it removes doubt about the number of significant digits in a measurement Suppose the volume of a gas is expressed as 2000 cm³.

We do know whether the measurement was made to one or to four significant digits. Suppose the measurement was actually made the nearest cm3. Then the volume 2000 cm³ is expressed to significant digits.

In scientific notation, we can indicate the additional significant digits by placing zeros to the right of decimal point. Thus, 2 x 10³ cm³ has only one significant while 2.000 x 10³ cm3 has four significant digits.

Once we have recorded measurements to the correct number of significant digits and expressed them in scientific notation, if appropriate, we are ready to use these measurements in calculations.

To determine the number of digits that should appear in the answer to a calculation, we will use two rules.

1. In addition and subtraction, the answer may contain only as many decimal places as the least accurate value used in finding the answer.

For example, if 345 is added to 27.6 the answer must be given to the nearest whole number. In adding a column of figures such as

677 + 39.2 + 6.23 + 722.43

the answer should be rounded off to the nearest whole number. The answer to the problem above is 722.

2. In multiplication and division, the answer may contain only as many significant digits as the least accurate value used to arrive at the answer.

For example, in the following problem (1.133 0)(5.126 000 00) =

the answer has five significant digits.

If you are using a calculator to obtain your numerical answer, you must be very careful. The calculator may give you an answer with eight or ten digits.

For example, in the problem 49.600 0/ 47.40, the answer may appear as 1.046 413 502. The answer must be rounded to the proper number of significant digits. In this case, the number of significant digits is four. Thus, the answer is 1.046.

Always double-check your answer against the data given. Report the answer only to the number of significant digits justified by the data.

2:10 A GENERAL APPROACH TO PROBLEMS One trait shared dy most chemists is the ability to solve prbolems. You will need to develop this ability during your study of chemistry. Skill in solving problems can be developed by practice. A good way to practice solving problems is to break the problem into three parts.

In Part One, decide what information you are given. Locate the starting material with which you will be working. Another way of expressing Part One is "Where am I?"

In Part Two, decide what is required of you. Make certain know what you are to find. Another way of expressing Part Two is "Where do I want to be?"

In Part Three, find a "bridge" connects what you are given to what is required of you. Part Three could also be expressed, "How do I get from where I am to I want to be?"

Parts One and Two require a careful reading and of the question or problem. The first time you read the problem concentrate on finding the starting point. Concentrate the second time on what you are required to find.

The "bridge" mentioned in Part Three comes from two sources, your background of general knowledge is the first source. The second source is the knowledge you will gain in your of chemistry.

Perhaps your chemical knowledge will not lead you to an immediate method of solving the problem. The knowledge you already have will be a guide to using textbook including the Table of Contents, the Appendices, the Index.

The text contains Example problems and solutions which you can use in solving problems. Learn to look for patterns in solving different types of problems. Then apply pattern to solving the problem at hand.

The solving of problems in chemistry is not an inherited talent. Everyone can learn the skill with practice. Be patient concentrate, and you will develop the skill.

2:11 CONVERSlON FACTORS

In section 2:1, the relationships between various prefixes were described. For example, the relationship between the centimeter and the meter is 1 m = 100 cm. The kilogram and the gram are related by the equation 1 kg = 1OOO g. Using these and similar relationships, we can convert a unit to any other related unit.

2:13 DENSITY

A less familiar, but common, scientific measurement is density. Density is mass per unit of volume. To measure density, we must be able to measure both mass (m) and volume (V).

Mass can be measured on a balance. The volume of a solid can be measured in different ways. For instance, the volume of a cube is the length of one edge cubed (multiplied by itself three times). The volume of a rectangular solid is the length times the width times the height.

The volume of a liquid can be measured in a clear container graduated to indicate units of volume. You will use graduated cylinders in lab to measure liguid volumes.

In density measurements of liquids and solids, volume is usually measured in cubic centimeters (cm³) or millileters (mL). Density, then, is expressed in grams per cubic centimeter (g/cm³). The units used to express density are derived units.

In equation form, density can be expressed as

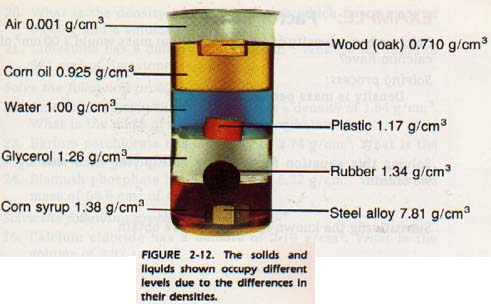
Densities of common materials are listed in Table 2-3. Such a table offers a convenient and accurate means of comparing tbe masses of equal volumes of different materials.

Note that the values given for gases are quite small. It is more practical to express gas density in g/m³ or g/L.

People sometimes say that lead is heavier than feathers. However, a truckload of feathers is heavier than a single piece of lead bucksbot. To be exact, we should say that the density of lead is greater than the density of feathers.

The density of a substance changes with changes in temperature. Ice floats in a glass of ice water because it is less dense than the liquid.

1. scientific work requires a quantitative approach. In other words, to investigate a phenomenon, certain characteristics must be measured.

2. Scientists use SI measurements. This system of measurement consists of seven fundamental units. SI units are particularly convenient because they are based on multiples of 10.

3. The most elementary measurements in science are those of mass, length, time, and temperature. The SI unit of volume is the cubic meter (m³). Speed is length per unit time.

4. Density is the mass of a substance in a unit volume of that substance. All three of these quantities are compound or derived.

5. Accuracy of a measurement is determined by the quality of the measuring instruments. Precision of a measurement is the relatiire error.

6. Any number can be expressed in scientific notation as M x 10ⁿ.

7. Scientific notation indicates clearly the number of significant digits. This notation is particularly helpful in multiplication and division.

8. In the factor-label method of problem solving, unit labels are treated as factors. This method makes conversion of units easier.

For a PowerPoint presentation Click Here.

Return to the Textbook Menu

Go to Textbook Assignments:

Return to the Big Chem Page