The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).

This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.

GASES AND THE MOLE

In Chapter 18, we examined the effect of temperature and pressure on the volume of a constant mass of gas. The principles hold true for any gas exhibiting ideal behavior. Different gases, however, have molecules and atoms of different masses. In this chapter, we will look at the effect of the number of particles on the other gas variables, particularly volume. We will also find out how to obtain mass measurements of gases at various temperatures and pressures.

19:1 DEVELOPlNG AVOGADRO'S PRlNClPLE

Suppose we place two different gases at exactly the same temperature and pressure in separate containers which have exactly the same volume. At a given temperature, all gas molecules will have the same average kinetic energy regardless of size or mass.

Massive molecules will travel slowly, lighter molecules will travel more rapidly. However, the average kinetic energy (1/2 mv²) will be the same for all. If the kinetic energies are equal, any difference in pressure exerted by the gases is determined by the number of molecules of each gas.

Since we have already said the two gases are at the same pressure, there must be an equal number of molecules in the two containers.

At equal temperatures and equal pressures, equal volumes of gases contain the same number of molecules. This statement is called Avogadro's principle, after Amadeo Avogadro.

When he proposed the principle, in 1811, the kinetic theory had not been developed. As we read in Section 5:2, Avogadro developed his principle to explain some of the observations made by Gay-Lussac. Gay-Lussac had observed that two gases always react in such a way that the combining volumes can be expressed in small whole numbers.

Proust had previously stated his law of definite proportions. Avogadro knew that one molecule of chlorine always united with one molecule of hydrogen. He also knew that two molecules of hydrogen chloride were formed.

He therefore concluded that equal volumes of gases must contain equal numbers of molecules, Avogadro's principle has been verified so often that it is sometimes called a law.

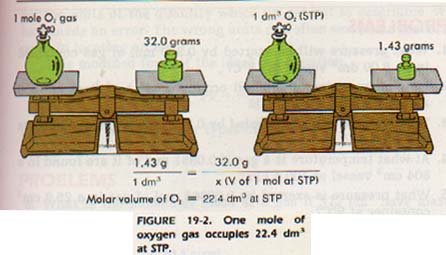
19:2 MOLAR VOLUME

One mole of any gas at STP will occupy the same volume as 1 mole of any other gas at STP. This volume is 22.4 dm³, (22.4 liters/mol) the volume occupied by 1 mole of any gas under standard conditions, is called the molar volume of the gas.

19:3 lDEAL GAS EQUATlON

We are now in a position to combine all four variables concerned with the physical characteristics of gases. These variables are pressure, volume, temperature, and number of particles. Charles' law states that volume varies directly as the absolute temperature. Boyle's law states that volume varies inversely as the pressure. Combining all the above factors gives us the ideal gas equation:

The equation PV = nRT is called the ideal gas equation. The value of the new constant R can be obtained by substituting into the equation a set of known values of n, P, V, and T. We know that standard pressure P is 1O1 kPa, molar volume V is 22.4 dm³, standard temperature T is 273 K, and the number of moles n is 1. So the constant R = 8.31 dm³•kPa/mol•K

This value for R is constant and can always be used if the units of the other quantities are not changed. We can determine the number of moles, n, in a quantity of a substance by dividing its mass by its formula mass. Any problem that can be solved by this equation can also be solved by direct application of the gas laws.

1. Avogadro's principle: At equal temperatures and pressures, equal volumes of gases contain equal numbers of molecules.

2. The molar volume of a gas is the volume occupied by 1 mole of the gas at STP; its value is 22.4 dm³ or 22.4 L/mol, for all gases.

3. The ideal gas equation is PV = nRT, where P = pressure, V = volume, n = number of moles, R = a constant, and T = kelvin temperature.

4. The molecular mass of a gas may be determined by using a modified form of the ideal gas equation.

5. A limiting reactant is a reactant which is completely consumed in a reaction. Any remaining reactants are said to be in excess.

6. In solving problems involving gas volumes, consideration must be given to the change of gas volume with change in pressure and temperature.

7. A gas which expands or is compressed does work or has work done on it.

More on Gases & Moles:

For a PowerPoint presentation Click Here.

Return to the Textbook Menu

Go to Textbook Assignments:

Return to the Big Chem Page