The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).

This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.

GASES

You already know many characteristics of gases because air is composed of gases. When we speak of a cubic centimeter of a solid or a hundred cubic centimeters of a liquid, we are referring to a definite amount of matter.

Both solids and liquids expand and contract with temperature changes. However, the change is usually small enough to ignore. This statement is not true for gases. The kinetic theory, as well as common experience, shows that a given amount of gas will occupy the entire volume of its container. When gases are heated, the change in their volume is large. Most solids and liquids subjected to the same temperature change would change very little in comparison.

According to the kinetic theory, a gas is made of particles which are in constant random motion. Gas particles are not held in a fixed position by the attraction of other particles as are those in a solid. These particles do not behave like those found in a liquid either. In a liquid, particles may change their relative position easily but their motion is restricted. This restriction occurs because particles of a liquid are held relatively close by van der Waals (intermolecular) forces .

The size of a gas molecule is insignificant when compared with the distance between molecules. Thus, we assume that the particles of a gas have no effect on each other. They are called point masses since they are considered to have no volume or diameter.

A gas composed of point masses does not actually exist. This imaginary gas, composed of molecules with mass but with no volume and no mutual attraction, is called an ideal gas. In the latter part of this chapter, you will study about real gases, and how they differ in behavior from ideal gases.

The number of gas particles in a volume of gas depends the pressure and temperature of the gas. Therefore, in quantities of gas, it is necessary to specify not only the volume but also the pressure and the temperature.

Scientists agreed standards of pressure and temperature were needed in order compare volumes of gas. Standard pressure is 101 kilopascals and standard temperature is O^oC. We indicate that a has been measured at standard conditions by the capital lettered STP (standard temperature and pressure).

Gas volumes are reported in the scientific literature as so many m³ or dm³ at STP. The system is convenient but what can we do if we must actually measure a gas in the laboratory when the pressure is 98.7 kilopascals and the temperature is 22^oC? In this chapter, we will describe how a measured gas volume can be adjusted to the volume the gas would occupy at STP.

18: 1 BOYLE'S LAW

We have seen that a gas exerts pressure on the walls of its container because gas molecules collide with the walls. The pressure exerted by a gas will then depend on two factors. The two factors are the number of molecules per unit of volume and the average kinetic energy of the molecules. A change in either of these factors will change the pressure exerted by the gas. If the number of molecules in a constant volume increases, the pressure increases.

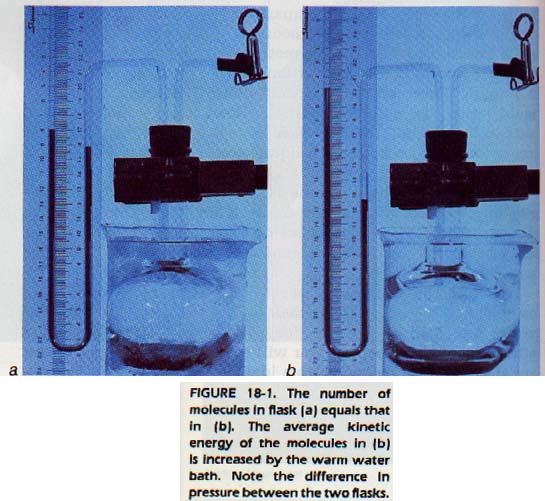
If the number of molecules and the volume remain constant but the kinetic energy of the molecules increases, the pressure increases.

Consider a container of gas with a movable piston in the top as shown in Figure 18-2.

Now imagine that the piston is lowered (without change in the number of molecules) and the temperature is kept constant. If the piston is lowered until it is half the original distance from the bottom, there will be only half as much space as before. The same number of molecules will occupy half the volume. The molecules will hit the walls of the container twice as often and with the same force per collision.

Since the same number of molecules in half the space is equivalent to twice as many in the same space, the pressure is doubled. We conclude that, at constant temperature, pressure varies inversely as volume. The product of pressure and volume is then a constant. The British chemist, Robert Boyle, arrived at this principle by experiment 300 years ago. This relationship is called Boyle's law.

Boyle's law states: If the temperature of a gas remains constant, the pressure exerted by the gas varies inversely as the volume.

18:2 APPLYlNG BOYLE'S LAW

It usually is not convenient to experiment with gases under standard conditions. Experiments are often carried out at room temperature and pressure. Since the temperature and pressure vary from day to day, experimental results cannot be compared so we shall have to make corrections with the gas law equations which will follow.

18:3 DALTON'S LAW OF PARTlAL PRESSURE

Chemists often obtain samples of gases by bubbling the gas through water. This procedure is known as collecting a gas over water. It is a useful system for collecting many gases, but the gas must be practically insoluble in water. Water vapor will be present in the gas sample.

How much pressure is exerted by a particular gas in a mixture of gases? John Dalton was the first to form a hypothesis about partial pressures. After experimenting with gases, he concluded that: the total pressure in a container is the sum of the partial pressures of the gases in the container: This statement is called Dalton's law of partial pressure.

In other words, each gas exerts the same pressure it would if it alone were present at the same temperature. When a gas is one of a mixture, the pressure it exerts is called its partial pressure. Gases in a single container are all at the same temperature and have the same volume. Therefore, the difference in their partial pressures is due only to the difference in the numbers of molecules present.

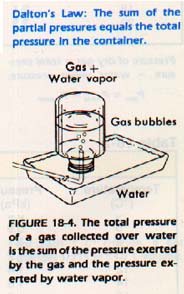
If a gas is collected over water, the pressure in the container actually includes the sum of the partial pressures of the gas and the water vapor. We know that each of the gases exerts the same pressure it would if it alone were present in the container. Therefore, if we subtract the value for water vapor pressure from the total pressure, the result will be the pressure of the gas alone. The vapor pressure of water at various temperatures has been measured. We need only to consult Table 18-2 to determine the partial pressure of water.

18:4 CHARLES' LAW

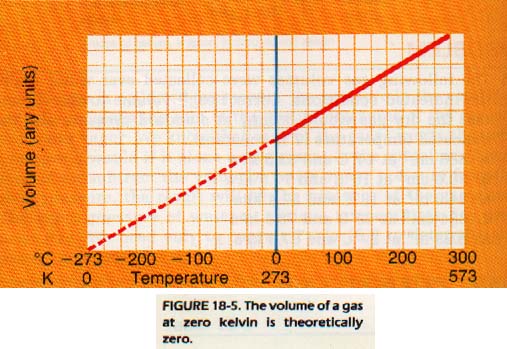
Jacgues Charles, a French physicist, noticed a simple relationship between the volume of a gas and the temperature. He found that, starting at O^oC, the volume of any gas would double if the temperature were raised to 273^oC (pressure constant). For each Celsius degree increase in temperature, the volume of the gas increased by 1/273 of its volume at O^oC. If the original volume (at O^oC) is expressed as 273/273 = 1, an increase in temperature of 273^o will result in a new volume of 273 + 273 / 273 = 1.

An increase in temperature of 1 C^o will result in a new 274/273, or a 1/273 increase in volume. Similarly, Charles found that a gas will decrease by 1/273 of its O^oC volume for each degree decrease in temperature. This finding would suggest at -273^oC, a gas would have no volume, or would disappear.

This temperature is called absolute zero. -273^oC.

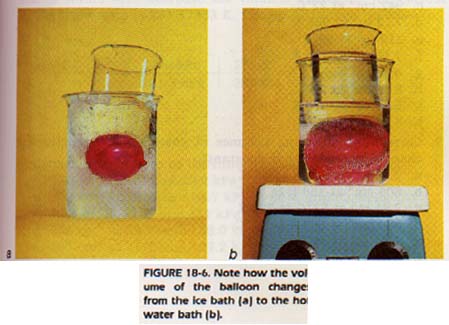
However, all gases liquid before they are cooled to this low temperature, and relationship does not hold for liquids or solids. The volume quantity of gas, held at a fixed pressure, varies directly the kelvin temperature. This relationship is called Charles' Law.

This experimental information led to the formation of the absolute or kelvin temperature scale. Thus far, we have defined the kelvin scale in terms of the Celsius scale. Now we in a position to define the kelvin scale directly. The zero of the kelvin scale is absolute zero.

The other reference point defining the kelvin scale is the triple point of water which defined as 273.16 K. You must remember that temperatures in Celsius must be converted to kelvin to work with gases: relationship is

18:5 APPLYlNG CHARLES' LAW

Charles' Law problems will be covered with the gas law equation which is coming up soon.

COMBlNED GAS LAW

Laboratory experiments are almost always made at temperatures and pressures other than standard. It is sometimes necessary to correct the laboratory volumes of gases for temperature and pressure. The correction is made by multiplying the original volume by two ratios, one for temperature and the other for pressure.

Since multiplication is commutative, it does not make any difference which ratio is used first. We may think of the process as correcting the volume for a pressure change while the temperature is held constant. Then, we correct for the temperature change while the pressure is held constant. The two changes do not have any effect on each other.

Here are the Combined Gas Laws:

For correcting to STP:

V is the measured volume.

P is the measured pressure in the lab in kPa (or mm of Hg).

T' is the measured temperature in K, (K = ^oC + 273^o).

P' will be standard pressure, 101 kPa (or 760mm of Hg).

T' will be standard temperature, 273 K.

V' will be the corrected volume at STP.

18:7 DlFFUSlON AND GRAHAM'S LAW

One of the basic ideas of the kinetic theory is that gas molecules travel in straight lines. However, a molecule is always colliding with other molecules. Therefore, its actual path is a series of straight lines connected end to end in no particular pattern.

If a bottle of a substance with a strong odor is opened on one side of the room, its odor can later be detected on the other side of the room. The molecules of the substance have traveled across the room by traveling in straight lines between collisions. However, they did not necessarily travel straight across the room. It took some time for them to reach the other side because they were colliding with air molecules.

This random scattering of the gas molecules is called diffusion. As the gas molecules diffuse, they become more and more evenly distributed throughout the room.

All gases do not diffuse at the same rate. We will assume that the rate of diffusion varies directly as the velocity of the molecules. This assumption is supported by experimental evidence.

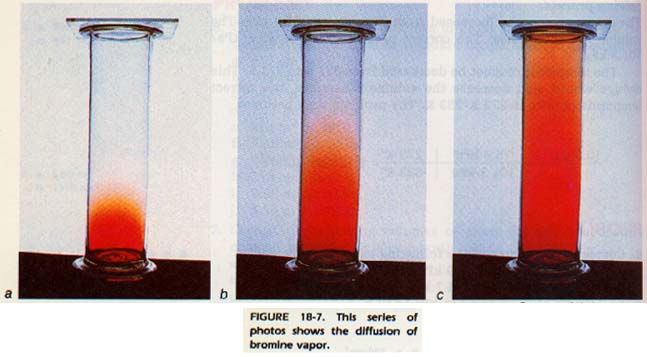
At the same temperature, molecules of low mass diffuse faster than molecules of large mass because they travel faster. They also will pass through a small hole (effuse) more rapidly than the molecules of higher mass.

In Section 15:4 we found that if two substances are at the same temperature their kinetic energies must be the same. Thus, KE₁ = KE₂. So

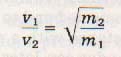
Where v₁ is the velocity of the lighter molecule (lower molar mass).

v₂ is the velocity of the heavier molecule (higher molar mass).

m₁ is the molar mass of the lighter molecule.

m₂ is the molar mass of the heavier molecule.

From this equation, we see that the relative rates of diffusion of two gases vary inversely as the square roots of their molecular masses. This relationship is true only when the temperature is the same for each. This principle was first formulated by a Scottish chemist, Thomas Graham, and is known as Graham's law. Graham's law states: The relative rates at which two gases under identical conditions of temperature and pressure will pass through a small hole varies inversely as the square roots of the molecular masses of the gases.

Hence the rate of diffusion is inversely proportional to the square root of the molar masses. This is Graham's Law of Diffusion.

18:8 GAS DENSITY

The density of gases and vapors is most often expressed in per cubic decimeter (liter). We express it in these units because usual density units, g/cm³, lead to very small numbers for

It is possible to calculate the density of a gas at any temperature and pressure from data collected at any other temperature pressure. Assuming that the number of particles remains same, a decrease in temperature would decrease the volume and increase the density. An increase of pressure would decrease volume and increase the density.

Remember that Density = mass / volume,

For a PowerPoint presentation Click Here.

Return to the Textbook Menu

Go to Textbook Assignments:

Return to the Big Chem Page