The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).

This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.

SOLIDS

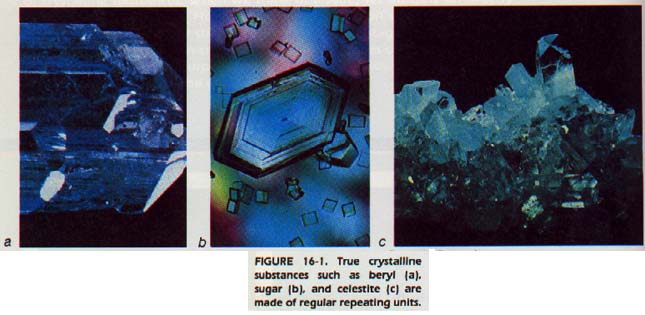
Have you ever examined table salt under a magnifying glass? If so, you would have seen that the crystals appear to be little cubes. The lengths of the edges may vary, but the angles between the surfaces are always exactly 90^o.

The systematic study of crystals began with Nicolaus Steno, in 1669. He observed that corresponding angles between faces on different crystals of the same substance were always the same. This fact was true regardless of the size or source of the crystals.

Steno's observation has been extended to all intensive properties (density, refractive index, face angles, and other similar properties. For example, a single crystal of the mineral beryl, Be₃A1₂Si₆O₁₈ weighing more than 40 tons was once unearthed in New Hampshire.

This huge crystal was found to be identical in intensive properties with any other beryl crystal. The size or mass of the crystal is not important. It can now be stated that the extensive properties of crystals vary while the intensive properties remain the same. (See Section 3:4 to refresh your memory on the difference between intensive and extensive properties.)

16:1 CRYSTALS

All true solid substances are crystalline. Apparent exceptions to this statement can be explained in either of two ways. In some cases, substances we think of as solids are not solids at all. In other cases, the crystals are so small that the solid does not appear crystalline to the unaided eye. The study of the solid state is really a study of crystals.

All crystals of a certain substance must be made of small units. These units are then repeated over and over as the crystal grows. Thus a crystal is defined as a rigid solid in which the particles are arranged in a repeating pattern. The shape and properties of these units are determined by the bonds between the particles.

Therefore, the bonding in the crystal partially determines the properties of the crystal. The units which compose a crystal are too small to be seen. Yet before any methods existed for studying crystal scientists suggested that crystals form by repetition of identical units.

Consider the patterns on wallpaper or drapery fabrics. These patterns are applied by rollers which repeat the design with each revolution. In a crystal, the forces of chemical bonding play the same role that the roller does in printing. They cause the basic pattern to be repeated over and over again. However, the "design" of a crystal must be composed of atoms, molecules or ions instead of ink.

The major difference between crystals and wallpaper is that the units in crystals are three dimensional. Those on wallpaper are only two-dimensional.

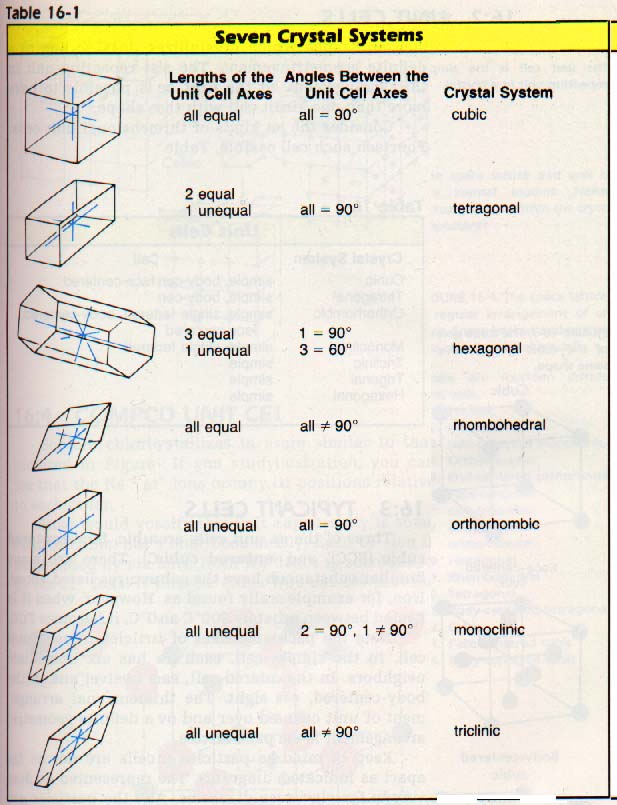
There is a relationship between the repeating units and the external shape of the crystal. Long ago, crystallographers classified crystals on the basis of their external shapes into seven "crystal systems".

16:2 UNlT CELLS

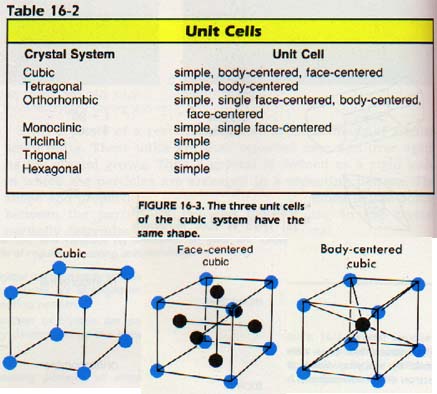
Each substance which crystallizes does so according to a definite geometric arrangement. The simplest repeating unit in this arrangement is called the unit cell. It is possible to have more than one kind of unit cell with the same shape. Consider the different kinds of three-dimensional unit cells. Fourteen such cells are possible, Table 16-2.

16:3 TYPlCAL UNlT CELL

Three of the simplest unit cells are the cubic, face-centered cubic (FCC), and body-centered cubic (BCC). There are many familiar substances which have the cubic structures listed above. \

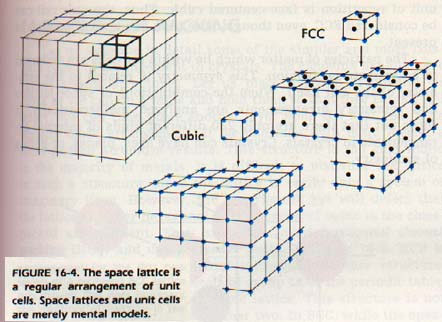
Iron, for example is generally found as BCC. However, when it is heated between approximately 900^oC and 1400^oC, it becomes FCC. Note the packing arrangement of the particles in each unit cell. In the simple cubic cell, each particle has six immediate neighbors. In the face-centered cell, each has twelve; and in the body-centered, each has eight. The three-dimensional arrangement of unit cells repeated over and over in a definite geometric arrangement is called a space lattice.

Keep in mind that the particles in the cells are not as far apart as indicated in the diagrams. They are represented as dots simply for clarity in those diagrams. Actually, the particles are extremely close.

It should also be pointed out that space lattices and unit cells have no real physical existence. The crystal is built of atoms, ions, or molecules. The space lattice is a mental model, or frame of reference, which helps us understand the facts of crystal structure.

16:4 COMPOUND UNlT CELLS

Sodium chloride crystallizes in a structure similar to that pictured in Figure 16-5. If you study the illustration, you can see that the Na⁺ and Cl^- ions occupy different positions relative to each other.

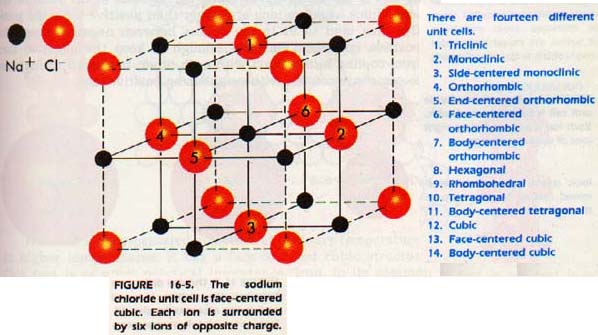
How would you classify this unit cell? It apparently is some form of cubic, but which one? Look more closely. Each C1^- ion is surrounded by six Na⁺ ions. Each Na⁺ ion in turn is surrounded by six C1^- ions. If you consider either alone, you can see that the unit of repetition is face-centered cubic. Thus, the unit cell be considered FCC, even though more than one kind of particle is present.

The particles of matter which lie within the cells are in a symmetrical fashion. This symmetry is related to the symmetry of the cell itself. When the combinations of space and symmetry arrangements are analyzed mathematically, turns out that there are only 230 different kinds of internal arrangements in crystals. Crystals can have axes, planes, or points of symmetry.

The particular crystal structure of an ionic compound such as salt is determined principally by the ratio of the radii of the ions. Since negative ions are larger than positive ions, the positive ions tend to fit in the spaces between negative ions. The positive ions must be large enough to keep the negative ions from coming into contact with each other, but small enough not to come into contact with neighboring positive ions.

16:5 CLOSEST PACKlNG

Let us examine in detail some of the simpler and more common types of arrangement in crystals. The elements usually have rather simple structures. Let us place a group of spheres as close as we can on a table and hold them so that they cannot roll apart.

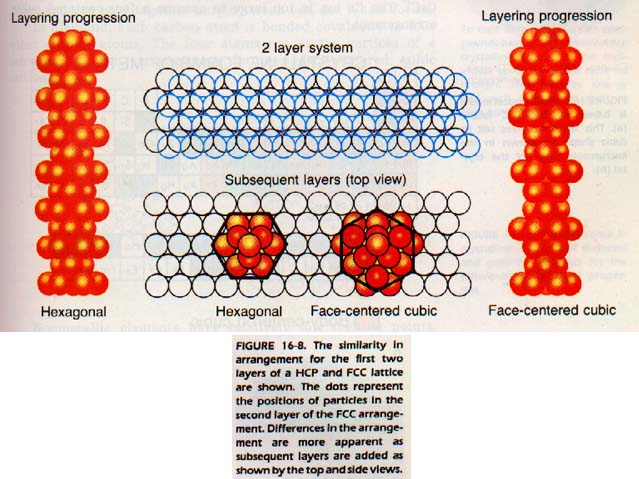
We can then place another layer upon the first one in an equally close arrangement. If we continue with more layers, a close-packed structure results. This structure is the kind found in the majority of metals. It is difficult to visualize the lattice in such a structure, since the lattice is really only a system of imaginary lines.

However, the experienced eye will detect that the lattice is either hexagonal or face-centered cubic in the close packed arrangement. They are often called hexagonal closest packing (HCP) and cubic closest packing, Figure 16-8. HCP is the one most frequently found in metals. Another structure, found particularly in the metals of group IA of the periodic table, is based on a body-centered cubic lattice. This structure is not quite so closely packed as the other two. In BCC, while the openings between the atoms are smaller, there are more openings.

Iron has a body-centered structure at ordinary temperatures. At higher temperatures, it has a face-centered cubic structure. This fact is of great practical importance. Iron, in its common form of steel, always contains a small amount of carbon. Carbon atoms are smaller than iron atoms, and at high temperatures they fit into the open spaces in the face-centered structure.

When the iron cools, it changes to the body-centered cubic form. In that form, the carbon atoms cannot fit into the smaller spaces. Either the iron lattice is distorted by the oversize carbon atoms, or the carbon separates out of the iron as iron carbide, Fe₃C. Iron and Fe₃C. crystals exist in many sizes and shapes.

The final structure of the crystal is determined by the percentage of iron and the rate of cooling. These differences in crystal structure result in the great versatility of steel as an industrial material. They also account for the fact that the properties of steel can be changed greatly by heat treatment.

Simple salts are those formed by the elements of Group IA (the alkali metals except for Cs) and the elements of Group VIIA (the halogens). These salts always have structures based on the FCC lattice. Figure 16-5 (above) shows a model of the sodium chloride structure, which is typical of this class of compounds. The same model would serve for other members of the group and also for many other binary compounds, like MgO and CaO.

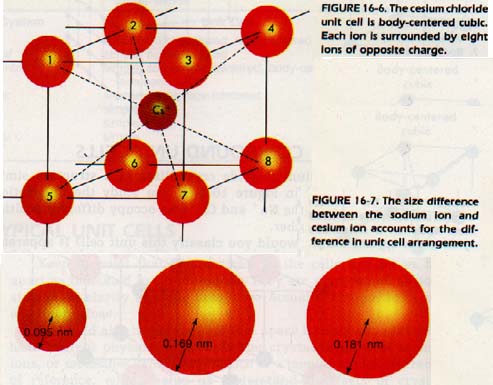
Note that it is impossible to distinguish an individual molecule of NaC1. Figure 16-6 (above) shows a body-centered cubic arrangement for CsCl. The Cs ion is too large to assume a face-centered cubic arrangement.

16:6 METALLlC ELEMENTS

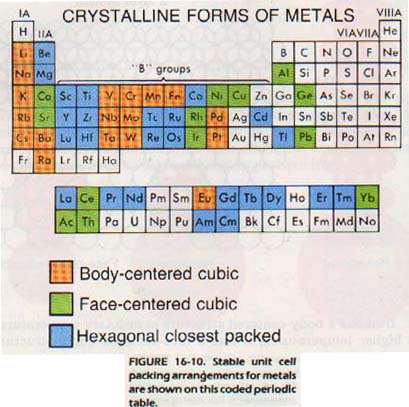
In Chapter 12 we discussed the metallic bond. At that point, we just "packed together" the positive metal ions before adding the electrons. How are the metal ions packed? Almost all metals are packed in one of three kinds of unit cells. These three are body-centered cubic (BCC), cubic closest packed (FCC), or hexagonal closest packed (HCP).

Figure 16-10 lists the unit cell arrangements for metals. The form given is the most stable at room temperature. Many metals, like iron, change their packing as the temperature rises. The general, though not universal, trend is toward the HCP arrangement.

NONMETALLlC ELEMENTS

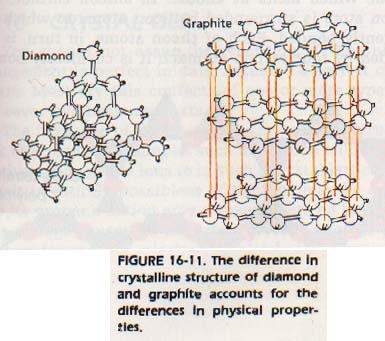
There are three crystal forms of carbon-- diamond, graphite and fullerines. Their structures are illustrated in Figure 16-11. You can see that in graphite, the atoms within each layer have a hexagonal arrangement. The atoms within each layer are held close by strong covalent bonds. The layers themselves are relatively far apart and are held together only by weak van der Waals (intermolecular) forces.

In diamond, each carbon atom is bonded covalently to four other carbon atoms. The four atoms are at the vertices of a tetrahedron. This arrangement forms a face-centered cubic lattice.

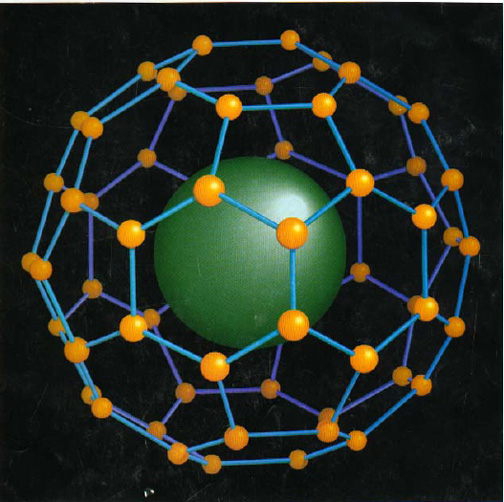
In fullerines we have a cage of carbon atoms in a soccer ball arrangement.

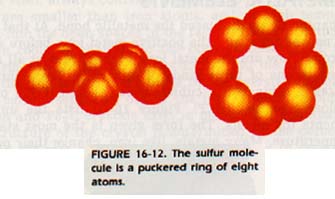
Nonmetallic elements have relatively low melting points. Elements like sulfur or iodine form crystals in which the lattice positions are occupied by molecules. The atoms of within the molecules are held together by covalent bonds. The molecules are attached to each other by weak van der Waals (intermolecular) forces.

In sulfur crystals, the S₈ molecule contains eight atoms arranged in a ring as shown in Figure 16-12. The atoms within the molecule are much closer to each other (0.108 nm) than they are to the atoms of neighboring molecules (0.37 nm). This lattice is orthorhombic.

16:8 MACROMOLECULES OR NETWORK CRYSTALS

In order to melt molecular solids, we need to overcome the van der Waals forces. Observations in the laboratory show that discrete molecular compounds have very low melting points. They range from -272^oC to about 400^oC.

There are some very large molecules which melt at even higher temperatures, but here we are concerned with the rule, not the exception. Still, we have not accounted for covalently bound substances with melting points in the range 1000^oC to 3000^oC.

An example is silicon carbide which melts at about 2700^oC. In silicon carbide, each carbon atom is surrounded by four silicon atoms to which it is covalently bonded. Each of these silicon atoms, in turn, is surrounded by four carbon atoms to which it is covalently bonded.

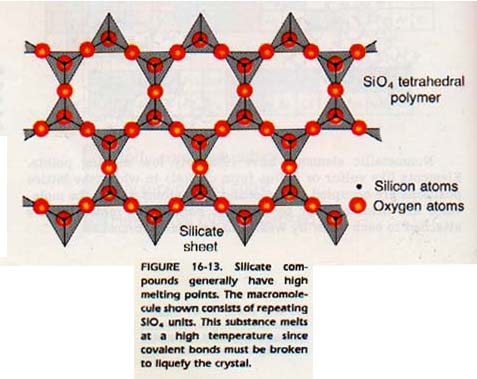
Thus, each atom in the crystal network is bonded to its four nearest neighbors. Silicon carbide has the same structure as diamond except every other atom is silicon.

We may think of the entire crystal as one giant molecule. In fact, this type of structure is often called a network crystal or a macromolecule. There are many substances composed of macromolecules. All of these substances have very high melting points. In order to melt the substance, we must break covalent bonds. These bonds are, on the average, about ten times stronger than van der Waals (intermolecular) forces.

16:9 BONDlNG AND MELTlNG POINT: A SUMMARY

Crystals composed of ions are held together by the electrostatic attraction of oppositely charged ions. These substances generally have high melting points.

In metallic crystals, the delocalized electrons bond the atoms tightly. Most metals have very high melting points.

Other covalently bonded substances can have low or very high melting points. If the atoms are part of a macromolecule such as diamond, the melting point will be high. To melt a macromolecule, an enormous number of covalent bonds must be broken. On the other hand, if atoms are covalently bonded in small, discrete molecules, the melting point will be low. These molecules are held to each other only by van der Waals forces which are easily overcome.

16:10 CRYSTAL DEFECTS

You should not assume that the repetition of the unit cell arrangement is perfect in all crystals. Actually, a perfect crystal is rare. Most crystals contain defects of one or more types.

We will cover two basic types of defects. The first type of defect occurs within the unit cell structure. Look at a plane of a simple crystal such as sodium chloride. The positive and negative ions alternate in such a crystal lattice. However, it is entirely possible that one of the ions may be missing from its proper position and occupy a space where no ion usually occurs.

This change causes an imperfect crystal. Another possibility is that an ion may be missing completely from its position in the lattice. If a defect of this type occurs, for every positive ion missing there must be a negative ion missing. This arrangement preserves the electrical neutrality of the crystal. It is sometimes possible for foreign ions, atoms, electrons, or molecules to occupy these spaces vacated by the normal ions of the crystal.

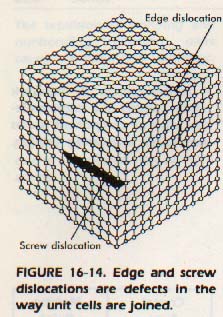
The second basic type of defect concerns the manner in which the unit cells are joined. These defects are called dislocations. In some crystals, an extra layer of atoms extends part of the way into a crystal. The resulting crystal is said to have an edge dislocation as shown in Figure 16-14. It is also possible for the particles to be slightly out of position. This defect is due to unequal growth while the crystal forms. Such a defect is termed a screw dislocation.

16:11 TRANSISTORS

Sometimes, defects in crystals are valuable. For example, in the manufacture of transistors, perfect crystals are "doped." That is, impurities are added deliberately.

Silicon and germanium (Group IVA) are the most common elements used in transistors. A pure crystal of either of these elements will conduct very little electricity. However, if a small amount of another element is added, current will readily flow through the resulting "doped" crystal.

A closer look at the bonding of these elements reveals why they behave as they do. Silicon and germanium, each with four electrons in the outer level, crystallize in a structure similar to that of the diamond. Thus, all four electrons are involved in bonding.

Recall from Chapter 12 that substances such as silicon and germanium are classed as semiconductors. The forbidden zone for semiconductors is small.

Arsenic atoms have five electrons available for bonding and gallium atoms have three. If arsenic atoms are introduced into a crystal of germanium, extra electrons are present. When a voltage is applied, the extra electrons in the lattice will move, Figure 16-15.

If on the other hand, gallium atoms are introduced, the crystal will be short of electrons. The resulting electron deficient lattice; however will also conduct electricity. It does so by moving electrons into the "holes" created by the gallium atom. Note that in both types of doping, the crystal is still electrically neutral.

Since their development in the late 1940's, transistors have been used in place of vacuum tubes in electronic circuits. Because of their small size, long life, and resistance to shock, they have revolutionized the communications industry. Computers, transistor radios, heart pacemakers, space probes, and microwave ovens are only a few of the many devices that transistors have either made possible or improved. Today's silicon microprocessor chips contain thousands of transistors.

l6:13 HYDRATED CRYSTALS

If solids crystallize from water solutions, molecules of water may be incorporated into the crystal structure. For some ionic substances, the attraction for water molecules is so high that the water molecules become chemically bonded to the ions.

Ions which are chemically bonded to water atoms are called hydrated ions. Crystals containing hydrated ions are called hydrated crystals. As we saw in Chapter 14, it is also possible for ions to be surrounded by, or coordinated with, solvent molecules other than water.

Many common chemical compounds are normally hydrated. It is possible to remove the water molecules from some hydrated crystals. It can be done by raising the temperature or lowering the pressure, or both.

The resulting compound, without the water molecules, is said to be anhydrous. Anhydrous means without water.

Some anhydrous compounds gain water molecules so easily that they can be used to remove water from other substances. They are called drying agents. Chemists refer to drying agents as dehydrating agents or desiccants.

Hydrated ions are chemically bonded to water molecules. Hydrated crystals contain hydrated lons.

Common drying agents: Calcium chloride, conc. H₂SO₄ , sodlum hydroxide. magnesium chloride.

Formulas for hydrated Compounds place the water of hydration following a dot after the regular formula. For example, CuSO₄ •5H₂O is the formula for a hydrate of copper sulfate that contains 5 moles of water for each mole of copper sulfate.

The ions of some anhydrous substances have such a strong attraction for water molecules that the dehydrated crystal will recapture and hold water molecules from the air.

Such a substance is called a hygroscopic (hi gruh sKAHP ihk) substance. Some substances are so hygroscopic that they take up enough water from the air to dissolve and form a liquid solution. These substances are said to be deliquescent (del ih KWEs uhnt).

The opposite process can also occur. Water of hydration may be spontaneously released to the air. A substance which releases water molecules to the air from the crystal is said to be efflorescent (efluh RES uhnt).

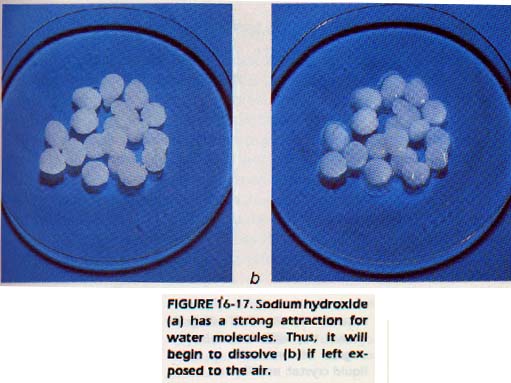
Special care is required in storing hygroscopic substances. You may have noticed that some reagents in the laboratory stockroom have hardened in the bottle. This action can be prevented by making sure bottles are closed tightly.

16: 14 LIQUID CRYSTALS

As we have seen, true solids are crystalline. Their constituent particles are arranged in a highly ordered manner. The arrangement is called "ordered" because the particles are spaced in a regular, repeating fashion in all three dimensions.

In Chapter 15, we saw that the structure of liquids was much less regular. Particles can actually change their positions in a liquid. The structure of a liquid is less ordered than the structure: of a solid. The disorder of the liquid extends to all three dimensions.

In general, when a pure solid is heated, it has a sharp melting point at a specific temperature. At that temperature the solid changes to a liquid and the order in all three dimensions is destroyed.

However, there are some solid materials which can lose their crystalline order in only one or two dimensions at the melting point. At a specific higher temperature, the remaining order will also be destroyed. Between these two transition temperatures, these materials retain some degree of order. These substances are called liquid crystals.

If they retain two dimensional order, they are usually called smectic substances. If they retain only one dimensional order, they are called nematic substances. There is a third class of liquid crystals (with two-dimensional order) which will not be considered here.

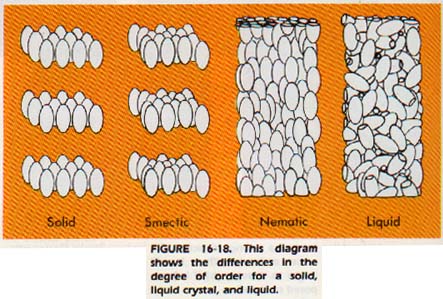
The structure leading to such properties has been determined. Liquid crystals are formed by long, rod like molecules arranged in a parallel manner. When the attractive force between layers of the molecules is overcome by heat energy, a smectic material results, with the layers remaining intact. If heat energy overcomes both layer attraction and end-to-end attraction, only parallel orientation remains. We then have a nematic material.

Substances in liquid crystal form are said to be mesomorphic that is, between solid and liquid. Mesomorphic materials exhibit anisotropy.

Anisotropic materials show different properties in different directions. We have already seen that graphite is anisotropic because of its bonding structure. Liquid crystals have optical and electrical anisotropy. Interestingly, along with other biological systems, both muscle fibers and nerve exhibit liquid crystal properties.

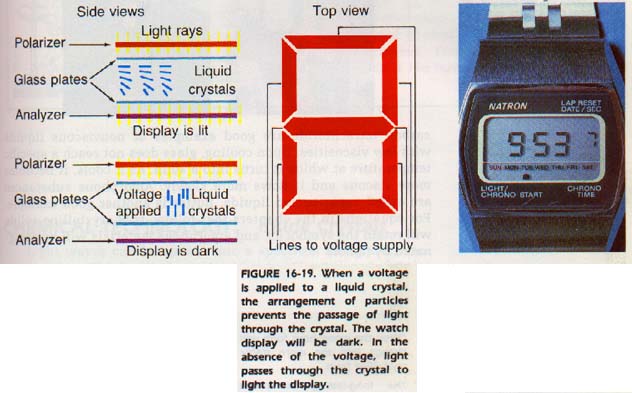
Some liquid crystals become transparent when subjected to a pulse of high-frequency current. Then if subjected to a low pulse, they become opaque. This property has led to the widespread use of liquid crystals for digital displays in and calculators.

16:15 AMORPHOUS MATERlALS

There are many substances which appear to be solids, but are not crystalline. Examination of their structure reveals a disordered arrangement of particles. These materials are said to be amorphous, or without crystalline form.

Glass is an excellent example of an amorphous material.

When glass is heated, it does not reach a point at which it suddenly becomes liquid. Glass does not have a fixed melting point as ice has. Rather, as glass is heated, it softens more and more and melts gradually over a wide temperature range.

The hotter it gets, the more easily the glass flows. The resistance of a liquid to flow is called its viscosity.

Glass and cold molasses are good examples of viscous materials. Water and alcohol flow and evaporate readily, they are said to be volatile. Volatile means easily vaporized.

Steno's law states that the corresponding angles between faces on different crystals of the same substance are always the same.

A crystal is a rigid body in which particles are arranged in a repeating pattern. The smallest unit of the repeating pattern is called the unit cell.

The repetition of the unit cell in a crystal forms an imaginary lattice of particles called a space lattice.

Many substances form crystals with a close-packed structure composed of layers of spheres packed closely.

Molecular substances form crystals in which the molecules are held together by weak van der Waals forces. These substances have low melting points and low boiling points. Some substances form macromolecular crystals which are characterized by very high melting points.

Crystal defects are lapses in the regular repetition of the unit cell arrangement. Defects can be a result of either missing particles which leave a hole or extraneous particles. Other defects are edge dislocations and screw dislocations.

The transistor is an example of a practical application of a crystal defect

Crystals which have the same structure and shape but different components are said to be isomorphous. A single substance which has two or more crystalline shapes is said to be polymorphous.

Anhydrous compounds which gain water molecules easily are called desiccants because they remove water from other substances.

A hygroscopic substance has such a strong attraction for water molecules that it will capture water molecules from the air.

A deliquescent substance is so hygroscopic that it takes enough water from the air to dissolve itself.

A substance which spontaneously releases water of hydration to the air from a crystal is called an efflorescent substance.

Liquid crystals are substances which retain some degree of order at their melting point. If they retain two-dimensional order they are called smectic. If they retain order in only one dimension they are called nematic.

Substances which seem to be solids but do not have a crystalline form are called amorphous substances.

The resistance of a liquid to flow is called its viscosity. The viscosity of substances usually decreases as the temperature increases.

More on Solids:

For a PowerPoint presentation Click Here.

Return to the Textbook Menu

Go to Textbook Assignments:

Return to the Big Chem Page