Heat Engines

Heat Engines

The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).
This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.
HEAT AND WORK
9.1 Mechanical Equivalent of Heat Since heat is a form of energy, it has the ability to do work. For example, you can warm your hands by briskly rubbing them together. You can heat up a nail by pounding it into a board with a hammer. And a tire pump gets hot when it is used vigorously.
As we noted in Section 1.13, Count Rumford and James Prescott Joule studied the relationship between heat and work in the 19th century. In experiments conducted between 1842 and 1870, Joule found that the heat produced by a given amount of mechanical energy is constant. The study of the quantitative relationships between heat and other forms of energy is called thermodynamics.
In this chapter we shall be concerned with the relationship of heat energy to mechanical energy. In discussing energy transformations, we shall also use the term internal energy. Internal energy is the total potential and kinetic energy of the particles of a substance.
These particles include molecules, ions, atoms, and subatomic particles. Heat is one form of internal energy.
Joule used an apparatus similar to that shown in Figure 9-2 to determine the relationship between mechanical energy and heat energy. The system on which work was done was a mass of water in an insulated vessel designed to reduce the escape of heat from the vessel to a minimum. A set of movable paddles on a shaft was turned by a falling mass connected to the shaft by a cord.
The paddles moved past fixed vanes, churned the water, and increased its temperature from Ti to some final value Tf. The work done on the water equals the loss of potential energy of mass m as it falls through a distance d, less the kinetic energy it possesses as it reaches the bottom.
The loss in potential energy is mgd. The final kinetic energy of the mass is1/2mv2. (In these experiments, v was small.) Hence, the amount of work, W, done on the system by the falling mass is
W = mgd - 1/2mv2
The amount of heat that would be needed to produce the observed temperature change in the water is
Q = mwcw(Tf - Ti)
Mechanical energy, or W, the work done on the system, is expressed in joules. Q is the equivalent heat energy expressed in calories. The results of many careful experiments have shown that
1 calorie = 4.19 joules
This equality is shown in Figure 9-3 and is known as the mechanical equivalent of heat.
Just as in the case of the hot brass chips in Count Rumford's cannon-boring experiments, it is possible to produce internal energy indefinitely in the Joule apparatus provided we continue to supply mechanical energy to it. Thus we must conclude that heat is a form of energy and not a substance.
9.2 First Law of Thermodynamics We can now broaden the statement of the conservation of energy in Section 1.13 to include internal energy as well as mechanical energy.
This generalization is known as the first law of thermodynamics: The quantity of energy supplied to any isolated system in the form of heat is equal to the work done by the system plus the change in internal energy of the system.
Thus the energy input to an isolated system equals the energy gained by the system plus the energy output in the form of work. We may also state the first law of thermodynamics as follows: When heat is converted to another form of energy or when other forms of energy are converted to heat, there is no loss of energy.
As an application of the first law of thermodynamics, let us assume that an amount of heat, Q, is added to a substance whose total internal energy is Ei. Generally we would find that the addition of this heat energy increases the internal energy of the substance to Ef and also causes the substance to do a quantity of work, W, on its surroundings. This can be stated algebraically as
Q = (Ef - Ei) + W
Q is positive when heat is added to the substance, and is positive when the body does work on surrounding objects. All quantities must be expressed in the same units either joules or calories.
In situations when no work is done by or on the substance, the change in internal energy equals the quantity of heat added to or removed from the substance. Adding heat to water that undergoes no change of phase cause each gram of water to increase in temperature by one Celsius degree for each calorie of heat added.
Here we neglect the very small amount of work involved in changing the volume of the water. We know that the internal energy of the water is changed because the temperature of the water is changed.
A process in which no heat is added to or removed from substance is called an adiabatic process.
In such a case, Q = O = (Ef- Ei) + W. Thus W = Ef - Ei. An example is the Joule experiment for determining the equivalent of heat described in the previous section.
When the vessel containing the water permits no heat to enter or leave during the churning process, the work done on water equals the change in its internal energy.
In another example let us assume that we have a quantity of air trapped in an insulated cylinder with a fitting but freely moving piston. When the air is compressed by pushing the piston into the cylinder, the change in the internal energy of the air must equal work done on it. This relationship is shown by the in volume, pressure, and temperature of the air.
9.3 Isothermal Expansion In nearly all situations involving gases, the gases are confined by barriers on which they exert a force and which, in turn, exert an equal and opposite force on the gases.
A gas may be under pressure in a storage tank or in a cylinder above a movable piston of an internal combustion engine. A quantity of air (an air mass) in the atmosphere is under pressure exerted by air around it.
In any of these cases, expansion of the gas requires it to do work against an external force; thus work is done on the external medium. On the other hand, the quantity of gas may be compressed by the action of an outside force; work may be done on the gas.
To calculate the work done by a gas in expanding, let us imagine the gas enclosed in a cylinder with a tight-fitting piston, as illustrated in Figure 9-4.
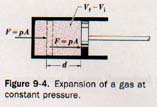
The piston rod is connected to a device on which it may exert a force. The force, F, acting on the piston due to the pressure, p, exerted by the gas on area A of the piston head is
F = pA
Suppose the piston is moved a distance d by the expanding gas in the cylinder. Suppose further that some heat is applied to the gas while the pressure remains constant during the expansion. The work done by the expanding gas in moving the piston will be
W = Fd = pAd
where the quantity Ad is the change in volume of the expanding gas. Thus the work done by the gas expanding at constant pressure is
W = p(Vf - Vi)
where Vf and Vi are the final and initial volumes, respectively, of the confined gas. We may conveniently show the work done by the gas expanding at constant pressure by using a graph, as shown in Figure 9-5.
On this graph volumes are plotted as abscissas and pressures as ordinates. The expansion at constant pressure is represented by a red horizontal line extending from Vi to Vf.
The work, W, done by the gas in expanding is given by the area between this line and the X axis and between Vi and Vf (the red portion shown in Figure 9-5). This graph is for the expansion of a gas at constant pressure.
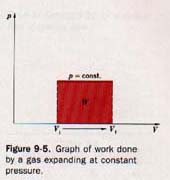
If the gas is compressed at constant pressure, the work done is represented in the same manner. It is considered negative, however, because the volume is decreasing as a result of work being done on the gas.
If during the expansion the pressure of the gas changes, the calculation becomes somewhat more complicated. Let us consider a situation in which sufficient heat is supplied to keep the temperature constant during an expansion. For a dry gas, the relationship between pressure and volume is given by Boyle's law
pV = constant
This relationship can be shown graphically, as in Figure 9-6. The area under the pV curve between Vf and Vi represents the work involved. This work can be computed by dividing the total volume change into a number of very small volume changes.
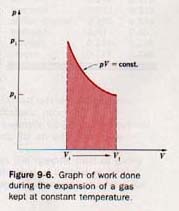
Each of these volume changes must be so small that the pressure remains practically constant for the change. The work associated with each minute change in volume is determined by multiplying change in volume by the pressure at the volume at the change takes place. The sum of all these quantities work equals the total work involved. A process that place at constant temperature is known as an isothermal process.
If the volume of an ideal gas increases at constant temperature, its pressure decreases. Similarly, if the volume of an ideal gas decreases at constant temperature, its pressure increases.
Since the internal energy of an ideal determines the temperature, there can be no change in the internal energy of an ideal gas during isothermal processes. However, work is done by a gas during expansion.
Since the volume occupied by the gas becomes greater, work is done on the gas molecules against external pressure. (In a real gas, some work is also done on the molecules, increasing their potential energy by moving them farther apart.)
The heat equivalent of the work done isothermally by an ideal gas during expansion must be absorbed from its surroundings.
In a similar manner, work must be done on an ideal gas during isothermal compression and the equivalent amount of heat must be transferred to its surroundings.
A sealed plastic bag containing air will increase in volume as the atmospheric pressure drops during an approaching storm, even if the room temperature remains, constant. The air in the plastic bag pushes out against the atmosphere, yet there are no temperature changes.
9.4 Adiabatic Expansion During an adiabatic expansion of an ideal gas, work is done just as it is during an isothermal expansion. Now, however, the equivalent amount of heat is not withdrawn from the surroundings, but is obtained at the expense of the thermal energy of the gas.
Thus during adiabatic expansion the temperature as well as the pressure of the ideal gas is lowered. Similarly, when work is done on a gas as it is adiabatically compressed, the heat equivalent of the work is not lost to the surroundings but is used to increase the internal energy of the gas.
Hence, during adiabatic compression both the pressure and the temperature of the gas increase. Adiabatic processes do occur in fast compressions when there is not enough time for the resulting heat to escape. An example of this process is the diesel engine, which will be described later in this chapter.
9.5 Specific Heats of Gases While the specific heat of a solid or liquid is a fixed value to several significant figures for the substance at a given temperature, this is not true for gases.
When heat is added to a mass of gas, its pressure, volume, or both may change, and its temperature may rise.
When the volume of a unit mass of gas is held constant as heat is added, the quantity of heat required to change the temperature of this unit mass of gas by 1 Co is called its specific heat at constant volume, cv.
When the pressure of the same unit mass of gas is held constant as heat is applied to raise its temperature 1 Co, the quantity of heat required is called its specific heat at constant pressure, cp.
The numerical value of cv differs from that of cp even though the same mass of the same gas is taken through the same temperature interval. The internal energy of the unit mass of gas must be changed by the same amount in each instance. Where the pressure is held constant, added energy must be provided to do the work required to produce the volume increase.
That is, work must be done on the movable part of the gas container or the surrounding atmosphere. This added work equals the pressure times the change in volume. As a result cp is greater than cv. In addition to increasing the internal energy, as evidenced by the increased temperature of the gas, some of the added heat energy is transformed into mechanical energy as a result of the expansion.
The same situation exists for liquids and solids. However, the amount of expansion is so small that the two specific heats are numerically the same to the number of significant figures with which we work, even in most research situations.
The values of cp and cv for some common gases at room temperature and atmospheric pressure are given in Table 9-1.
HEAT TRANSFER MECHANISMS
9.6 Efficiency of Heat Engines The processes occurring in the operation of an engine that converts heat energy into mechanical work are complex. However, we can simplify things by replacing the actual heat-engine cycle with an ideal cycle that can produce the same transformations of heat and work. We need not be concerned here with the fact that there are many different types of heat engines utilizing a variety of working substances such as steam, a mixture of fuel and air, or a mixture of fuel and oxygen.
In an engine, the working substance is taken through a series of operations known as a cycle. The result is that some of the heat supplied to the substance from a high temperature source is converted into work that is delivered to an external object. For example, high-temperature steam drives a turbine that in turn does work on an electric generator. Experimental and theoretical evidence indicate that not all the heat supplied to the engine can be converted into work. The heat that is not converted into work is delivered by the engine to some external reservoir at lower temperature. Such a reservoir is called a heat sink. It is a system that absorbs the exhausted heat, preferably without a significant increase in its own temperature.
In an ideal heat engine, the working substance is a gas that is returned at the end of the cycle to its original pressure, volume, and temperature conditions. There is no permanent loss or gain of internal energy; the internal energy of the working substance remains unchanged.
In the operation of an ideal heat engine, a quantity of heat, Q1, is delivered to the engine during the beginning of a cycle. This heat comes from a high-temperature heat source. The engine performs an amount of work, W, on some outside object and exhausts an amount of heat, Q2, to a low-temperature heat sink. Low temperature in this case means any temperature below that of the heat source, and ideally much lower. Applying the first law of thermodynamics to this cycle,
W = Q1 - Q2
The thermal efficiency, e, of the heat engine is defined as
e = work done during one cycle / heat added during one cycle
e = W / Q1
or
e = 1 - T2 / T1
From this equation we can see that the efficiency of heat engine may be increased by making the temperature of the heat source as high as possible and the temperature of the heat sink as low as possible.
From experience we know that gasoline and steam engines expel some heat during the exhaust part of the cycle. The efficiency of any real heat engine will be less than efficiency of an ideal heat engine because of heat loss in engine parts and friction
It is interesting to note that the efficiency of steam engines has increased from 0.17% for the first steam engine of the seventeenth century to over 40% for the used in modern power plants.
9.7 Second Law of Thermodynamics It was noted the previous section that not all the heat supplied to a engine can be converted into mechanical work. This fact is true for all types of heat engines and is the basis far-reaching generalization known as the second law thermodynamics, which was first formulated by the man physicist, Rudolf Clausius (1822-1888): It is not possible to construct an engine whose sole effect is the extraction heat from a heat source at a single temperature and the conversion of this heat completely into mechanical work.
Thus if a engine takes a quantity of heat from a heat source at a high temperature, it must transfer some of this heat to a sink at a lower temperature.
One interpretation of the second law of thermodynamics is that it is impossible to attain the absolute zero temperature. There is simply no place to which heat be transferred in order to cool a substance to exactly 0oK.
Values only a few thousandths of a degree above absolute zero have been attained. The experimental difficulties increase enormously as still lower temperatures are sought. The unattainability of absolute zero is sometimes called the third law of thermodynamics.
Some have considered extracting heat from the internal energy of the ocean and using this to operate the engines of a ship. If the water surrounding the ship is considered a heat source at a single temperature, the second law of thermodynamics indicates that it would be impossible to operate the engines of the ship from the internal energy of the sea water.
It also follows from the second law of thermodynamics that transfer of internal energy from a low-temperature heat source to a high-temperature heat sink requires work. This type of internal energy transfer takes place in refrigerators, air conditioners, and heat pumps.
In order to express the second law of thermodynamics in quantitative form, we must be able to measure the amount of mechanical work a system can do. For example, consider placing a hot and a cold body in thermal contact. After a time they will reach thermal equilibrium; the two bodies will come to the same temperature.
There is no loss of energy in the process, but the system as a whole loses its capacity for doing work. (The temperature of the environment is disregarded in this discussion.) A heat engine connected between the two bodies before the bodies were placed in contact could have done useful work. After contact of the two bodies, when a temperature difference no longer exists between them, work cannot be done by an engine connected between the two.
9.8 Entropy

If the change in entropy is positive, the entropy of the system is increased. This is an example of an irreversible process in which a loss of capacity for work results in an increase in entropy for the system.
It can be shown that for any transformation occurring in an isolated system, the entropy of the final state can never be less than that of the initial state. Only in cases where the transformation is reversible will the system undergo no change in entropy.
The second law of thermodynamics can now be restated as the law of entropy: A natural process always takes place in such a direction as to cause an increase in the entropy of the universe. In the case of an isolated system it is the entropy of the system that tends to increase.
All natural processes are irreversible and involve increases in entropy. Thus the second law of thermodynamics is equivalent to the statement that the entropy of the universe is increasing, and the first law of thermodynamics is equivalent to the statement that the total energy of the universe is constant.
Heat can be considered disordered energy. An example of ordered energy is a flying rifle bullet that has kinetic energy. When the bullet is stopped suddenly by impact, the energy of its motion is transformed to random motion of atoms. This disordered energy is evidenced by the heating of both the bullet and the area of impact.
Work involves orderly motion. But when work is done against friction and is dissipated into internal energy, the disorderly motion of molecules is increased. There is an accompanying increase in disorder. The tendency to acquire maximum randomness.
There are many examples in nature where energy processes are observed to go toward a state of greater disorder. The melting of an isolated crystalline solid is an example. When heat is added, the system goes from a well-ordered array of molecules in a crystal to a less well-ordered array of molecules in a liquid without a change in the temperature of the sample.
Entropy may thus be thought of as a measure of the order-disorder in the system. Most natural processes proceed toward a state of greater entropy as well as toward increased disorder. It is not surprising to note that physicists have found a connection between the thermodynamic concept of entropy and the statistical concept of disorder.
Two quantities can be used to describe heat. One quantity describes the energy and is measured in calories or joules. The other quantity describes the amount of disorder and is expressed as entropy, which is a mathematical concept.
9.9 Steam Engines The earliest known devices in which heat is converted to work were described by Hero of Alexandria in the first century A.D. In the so-called Hero's fountain, heated air was used to expel water vertically out of a container. In another device, known as the aeolipile, steam generated in a boiler passed through tubes into a sphere and out through nozzles that were mounted tangentially to the sphere. The reaction force of the steam leaving the nozzles made the sphere rotate. Neither of these devices had much practical value, however.
The first practical steam engine was built in England in 1712 by Thomas Newcomen (1663-1729). In the design of the Newcomen engine, steam was directed against a movable piston inside a cylinder. A rod that was connected to the moving piston activated a water pump or some other mechanical device. James Watt and others made important improvements on the steam engine, which became a major impetus for the Industrial Revolution.
Figure 9-11 is a cross-sectional view of a double-acting steam engine. As the name implies, steam enters the cylinder through a sliding valve and pushes the piston first in one direction and then in the opposite direction. In some modern steam engines, pressures of more than thirteen kilopascals are used. (The pascal, or Pa, is a derived SI unit that equals a newton per square meter.)

Reciprocating Steam Engine
The efficiency of the steam engine can be increased by arranging several cylinders in tandem, so that the steam leaving the first cylinder is used to push the piston in a second cylinder, and so on. Some compound steam engines of this type in large ocean liners have power outputs of more than 11,000 kilowatts. Ah, the Titanic!
Steam engines have been largely replaced by other power sources, such as the steam turbine and the gasoline engine. But a small steam engine is more efficient than a small steam turbine, and where large supplies of steam are required for other purposes, it can be economically feasible to use a steam engine to drive pumps and compressors.
9.20 Steam Turbines In one type of steam turbine, steam at a high temperature and high pressure is directed through nozzles against a set of cupped blades attached to a wheel. This arrangement is called an impulse turbine. The sideways component of the force of the steam against the blades causes the turbine wheel and the shaft on which it is mounted to rotate. Small impulse turbines may be made to move at rates of more than 10,000 revolutions per minute.
In a second type of steam turbine, high-pressure steam passes through alternating sets of movable and vanes, as shown in Figure 9-12. This is called a reaction turbine

A single reaction turbine may contain forty or more pairs of movable and fixed sets of vanes. The fixed vanes are attached to the housing of the turbine, while the movable vanes are connected to a single shaft. The diameters of the turbine blades are made increasingly larger from the inlet to the outlet part of the engine, so that the energy of the expanding steam is transferred more efficiently. This arrangement can be seen in Figure 9-13.

Various combinations of steam turbines are used today for ship propulsion and for driving generators in electric power plants. In a large modern steam turbine, steam may enter at a pressure of more than 240 kilopascals and a temperature of over 560oC.
This obviously requires the use of special alloys that can withstand extreme conditions of temperature and pressure. As explained in Section 9.6, a large difference between the input and exhaust temperatures increases the efficiency of a heat engine. Such steam turbine-generator combinations with power outputs of more than 1,000,000 watts are in use today.
9.11 Gasoline Engines Steam engines and steam turbines are examples of external combustion engines. That is, the fuel burns outside the engine and the heat is transferred to a cylinder or turbine chamber by means of steam.
In an internal combustion engine, the fuel burns inside the cylinder or engine chamber. This requires the use of a fuel that does not leave appreciable amounts of solid combustion products in the engine.
Combustible vapors are therefore used in most internal combustion engines. The gasoline engine, which is the most widely used of all heat engines, is an internal combustion engine. Figure 9-14 shows the sequence of events in a four-stroke gasoline engine. As the piston moves down, (A), air and gasoline vapor are brought into the cylinder through a valve. As the piston moves up again, (B), the valve closes and the air-vapor mixture is compressed to a fraction of its original volume. This compression causes the temperature of the mixture to rise. A spark then starts a chemical reaction between the gasoline vapor and the oxygen in the air, (C).
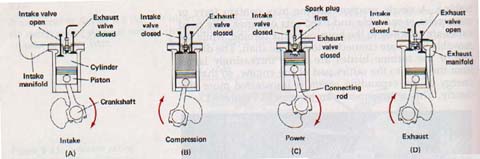
Heat produced by the chemical reaction increases pressure of the gas in the cylinder. Changing some of internal energy into mechanical energy causes the pressure of the gases to decrease, but not to a temperature low as the temperature of the outside air. The heat was added from the chemical reaction was partly converted to work and partly used to increase the internal energy of the gases that escape through the exhaust.
The number of cylinders and their arrangement in a gasoline engine may vary, depending on the application.
9.22 Diesel Engines In 1895, the German inventor Rudolf Diesel (1858-1913) developed an internal combustion engine that does not require spark plugs to ignite the fuel.
The heat of compression of the air inside the cylinder is sufficient to produce ignition. The fuel is injected at the time of maximum compression. The heating of the air during compression in a diesel engine is an example of an adiabatic process.
A diesel engine has a low power-to-weight ratio, but it is more efficient and can burn a lower grade of fuel than its gasoline counterpart. The diesel engine is also known for its reliability and durability. A small, single-cylinder diesel engine may have a power output of less than five kilowatts. Larger versions are used in buses, trucks, tractors, and locomotives. A diesel engine used for ship propulsion or in an electric-generating plant may have twelve cylinders, a piston diameter of more than seventy centimeters, a stroke of over one hundred centimeters, and develop 7500 kilowatts.
9.13 Gas Turbines The gas turbine is another type of internal combustion engine. In a gas turbine, a large volume of air is continually drawn into a compressor, where its pressure is increased. This compressed air then flows into a combustion chamber, where the fuel is injected and burns with a continuous flame. Only part of the compressed air is needed for complete combustion of the fuel.
From the combustion chamber the hot combustion gases and heated air expand and move at great speed, first through a turbine and then through the exhaust nozzle. Some of the energy imparted to the turbine is used to drive the compressor. The remaining energy may be taken from the shaft of the engine to run an electric generator or some other machine.
The efficiency of a gas turbine is rather low, partly be cause the temperature is not as high inside the engine as it is in a reciprocating engine.
Very high temperature would cause deterioration in the turbine blades. A gas turbine is also less efficient than a steam turbine, since more work is required to compress the air in a gas turbine than to pump the water needed for the steam in a steam turbine.
A gas turbine is most efficient at high velocities and under maximum load. Gas turbines are presently used to power fast ships and trains, to pump gas through long distance pipelines, and to generate electricity.
Used conjunction with jet engines (which are described in next section), gas turbines also power all but the lightest and slowest of today's aircraft.
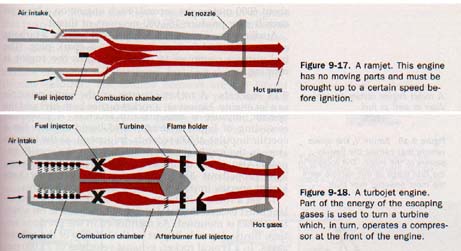
9.24 Jet Engines Hero's aeolipile (Figure 9-10) the first jet engine. As the steam leaves the nozzles of aeolipile, the reaction force turns the sphere on which nozzles are mounted. The reaction force in a jet engine is called thrust. (Thrust is not produced, as is often imagined by the push of the escaping gases against the surrounding atmosphere.) The simplest type of modern jet engine is the ramjet. Ramjet has no moving parts. See Figure 9-17. Air is at increased pressure into the combustion chamber, fuel is added and burns. The hot combustion gases heated air rushing out through the jet nozzle produce unbalanced reaction force that moves the engine forward.
SUMMARY
The study of the quantitative relationship between heat and other forms of energy is called thermodynamics. One calorie of heat is equal to 4.19 joules of mechanical energy. The first law of thermodynamics states that the quantity of heat supplied to a system is equal to the work done by the system plus its change in internal energy. The expansion of a gas always tends to increase.
A heat engine converts heat energy into mechanical energy. Steam engines and steam turbines are external combustion engines. Gasoline engines, diesel engines, gas turbines, jet engines, and rockets are internal combustion engines. Unlike other engines, a rocket contains an oxidizer as well as fuel. The performance of rocket propellants is measured in terms of specific impulse.
The expansion of a gas may be an adiabatic or an isothermal process. Adiabatic processes are those in which no heat is added to or removed from a substance. Isothermal processes take place at constant temperatures. The specific heat of a gas varies with temperature.
The efficiency of an ideal heat engine increases as the difference between the temperatures of the heat source and heat dynamics states that it is impossible to make an engine that will extract heat from a heat source at a single temperature.
The amount of energy that cannot be converted into mechanical work is related to entropy. The change in entropy of a system is equal to the amount of heat added to the system divided by its Kelvin temperature. The entropy of a system always tends to increase (maximum randomness).
VOCABULARY
adiabatic process, aeolipile, entropy, external combustion engine, first law of thermodynamics, gasoline engine, heat pump, heat sink, heat source, internal combustion engine, internal energy, isothermal process, mechanical equivalent of heat, pascal, second law of thermodynamics, steam engine steam, turbine, thermodynamics.
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester