for the Research Text
First Semester
Chapters 1-9
He
Here are the Answers to the Problems.
The problems listed are the ones that we must do in our portfolios.
Here are the Assignment Numbers.
Quick Assignment Finder
Do not click here until the page is completely loaded!!!
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Questions GROUP A
1. What are the disadvantages of using fossil fuels as energy sources?
2. List as many present and future applications of computers as you can.
4. What is meant by a theory?
5. How does a hypothesis become part of a law?
6. (a) Define the term "laboratory." (b) How does your school's physics laboratory fit this definition?
7. Distinguish between science and technology.
Questions GROUP B
9. Edison once said: "Genius is 1% inspiration and 99% perspiration." Explain this remark in terms of the work of scientists and technologists.
10. How does the work of Kepler illustrate the scientific method?
11. Define the term "certainty" as it relates to science.
12. List questions and problems that, in your opinion, do not fall into the realm of science.
Questions GROUP A
1. How does the mass of an object on the earth compare with the mass of the same object on the moon?
2. (a) Distinguish between mass and mass density. (b) Distinguish between inertial and gravitational mass.
3. (a) Distinguish between properties and conditions, (b) Give examples of each.
4. (a) What is the source of energy in an automobile? (b) ) How is the energy transformed?
5. Classify the following as having mainly potential or mainly kinetic energy: (a) gasoline, (b) water behind a dam, (c) a moving car, (d) a spaceship in free flight, (e) gunpowder.
6. What limits the amount of heat energy that can be produced by the boring of a cannon barrel?
7. State the law of conservation of energy.
8. Give two meanings of the equation E = mc2.
9. What is meant by the wave-particle duality of nature?
10. Briefly describe the four subdivisions of physics.
Questions GROUP B
11. How can Figure 1-7 be used to find the mass of the balance pan used the experiment?
13. Could a platform balance be used in a spaceship in free flight? Explain.
14. Why are work and energy in the same units?
15. State a fact to support the caloric theory.
16. Why does it become increasingly difficult to increase the speed of an object as it approaches the speed of light?
17. In general, objects expand when heated. (a) How does this phenomenon show that heat is a form of energy? (b) Modify your explanation fit objects that contract upon being heated.
18. On the basis of Count Rumford's observations and conclusions about heat, can you explain how his experimentation led to the development by Joule of the mechanical equivalent of heat?
Questions GROUP A
1. What makes the metric system convenient to use?
2. What is the relationship between a physical quantity and a unit of measure?
3. List the seven fundamental units of measure.
4. List three derived units of measure and their related physical quantities.
5. What is meant by SI?
6. Describe the standard of length.
7. How are the cubic centimeter and the liter related?
8. Why is the standard kilogram an object instead of a laboratory process?
9. Distinguish between the mass and weight of an object.
10. How is the standard for the second obtained?
Questions GROUP A
1. Distinguish between the accuracy and precision of a measurement.
2. How does absolute error differ from relative error?
3. List four ways of expressing the precision of a measurement.
4. State the rule for determining the number of significant figures in the sum of added measures.
5. List three different cases in which a zero is not a significant figure.
6. How many uncertain figures should a correctly written measurement contain?
7. What is the advantage of using scientific notation?
8. (a) What is the shape of the graph of two quantities that are in direct proportion? (b) in inverse proportion?
9. Distinguish between a basic equation and a working equation.
10. Define "dimensional analysis."
11. What is meant by a "check for reasonableness" in solving a physics problem?
12. Distinguish between a scalar quantity and a vector quantity.
13. How is the resultant of two vectors determined when they are not acting along a straight line?
14. Describe two ways in which the resultant of three or more vectors can be found.
Problems GROUP A p 37
1. How many significant figures are there in each of the following numbers? (a) 173.2; (b) 205; (c) 4000; (d) 0.025; (e) 700; (f) 0.09050.
2. Write each of the numbers in Problem 1 in scientific notation form.
3. Write each of the following numbers in scientific notation form:
(a) 175,000,000
(b) 602,300,000,000,000,000,000,000
(c) 0.000047
(d) 0.000,000,000,000,000,000,000,000,672,39
4. What is the order of magnitude of each of the numbers in Problem 3?
5. A substance has a mass density of 0.20 g/cm3. What is the volume in cm3 of a 100-g sample of the substance?
6. A sample of maple wood has a mass of 40 g. Read the volume of the sample from Figure 2-11.
7. The time required for a 100-km trip is 1.5 hours. Read the average speed from Figure 2-12.
8. Give the order of magnitude of the answer for each of the following calculations:
(a) (6.1 x 108)(3.2 x 10-2)
(b) 5.92 x 10-2 / 5.37 x 108
(c) (65)(32 x 10-5)
(d) (2.35)(0.45)(546) / (379)(4.3 x 104)
Questions GROUP A
1. (a) Define displacement (b) Define motion
2. (a) Define speed. (b) Distinguish between average and instantaneous speed. (c) What are the units of speed in the metric system?
3. (a) What is velocity? (b) Distinguish speed and velocity.
4. (a) Describe the motion of an object that has uniform velocity. (b) Describe the motion of an object that has variable velocity.
Questions GROUP B
5. Why is speed a scalar quantity but velocity a vector quantity?
6. How can the magnitude and direction of the resultant of two velocities be determined?
7. (a) Does a change in the speed of an object always produce a change in its velocity? (b) Does a change in the velocity of an object always indicate a change in its speed? Explain.
8. In a graph of variable velocity, what is the meaning of the changing slope of the line?
Problems GROUP A
Note: Problems 2 through 6 should be (a) graphically and (b) trigonometrically.
1. The highway distance from Indianapolis to Denver is 1712 km. If the driving is 29.25 hr, what is the average for the trip?
2. A motorboat travels 25 km/hr in still water. What will be the magnitude and direction of the velocity of the boat if it is directed upstream on a river that flows at the rate of 4 km/hr?
3. An airplane has a velocity, with respect to the air, of 825 km/hr northward. What is the velocity of the airplane with respect to the ground if the wind is blowing with a velocity of 35 km/hr southward?
4. A person can row a boat at a speed of 5.0 km/hr in still water. The person heads directly across a river that flows at a speed of 3.5 km/hr. Determine the magnitude and direction of the boat's resultant velocity.
5. An airplane flies westward at 650 km/hr. If the wind has a velocity of 40.0 km/hr northward, determine the magnitude and direction of the resultant velocity.
6. An airplane is to maintain a velocity of 475 km/hr in a direction 45.0o north of east. If the wind velocity is 50.0 km/hr 45.0osouth of east, what should be the magnitude and direction af the velocity of the airplane to offset the effect of the wind?
Problems GROUP B
Note: Problems 7 through 9 should be solved (a) graphically and (b) trigonometrically.
7. Determine the magnitude and direction of the resultant velocity of 75.0 m/s, 25.0o east of north, and 100.0 m/s, 25.0o east of south.
8. A boat is to cross a river on a course directed 20.0o upstream to a dock 815 m distance in 10.0 min. If the flows at a speed of 3.0 km/hr, at what angle upstream must the boat be headed and what must be its speed in km/hr relative to the moving water?
9. An airplane must fly at a ground speed of 425 km/hr in a direction of 10.0o east of south to be on course on schedule. If the wind velocity is 25.0 km/hr 40.0o east of north, in what direction and at what speed relative the air must the pilot fly?
Questions GROUP A
Acceleration is a change in velocity. It can be positive or negative.
1. (a) What is acceleration? (b) Why is the unit of time squared in measuring acceleration?
3. Define the following: (a) uniform acceleration; (b) variable acceleration; (c) uniform deceleration; (d) variable deceleration.
4. What effect does the force of gravity have, on a baseball thrown directly upward?
5. Explain instantaneous acceleration?
6. What equation relates final velocity to initial velocity, acceleration, and elapsed time?
7. How can displacement be calculated when the initial velocity, final velocity, and elapsed time are known?
8. Give an example of an object moving at high speed with zero acceleration.
9. Give an example of an object starting with zero speed and high acceleration.
Problems GROUP A p55
Note: Whenever necessary, use g = 9.80 m/s2. Disregard the effect of the atmosphere.
1. If a ball is dropped and attains a velocity of 29.31 m/s in 3.00 s, what is the acceleration due to gravity?
2. An automobile can be accelerated from 95 km/hr to 142 km/hr in 8.1 s. What is the acceleration?
3. A large rock is dropped from a bridge into the river below. (a) If the time required for it to drop is 1.7 s, with what velocity, in m/s, does it hit the water? (b) What is the height, in meters, of the bridge above the water?
4. (a) How many seconds does it take for a metal ball to drop 145 m from rest? (b) What velocity does it attain?
5. An object with an initial velocity of 20.0 cm/s is accelerated at 8.0 cm/s2 for 5.0 s. (a) What is the total displacement? (b) What is the displacement during the fifth second?
6. What velocity is attained by an object that is accelerated at 0.30 m/s2 for a distance of 54 m if its initial velocity is 0.50 m/s?
7. (a) If the brakes of an automobile can decelerate it at 7.00 m/s2, what time is required to reduce the velocity of the automobile from 157.0 km/h to 75.0 km/hr. (b) How many meters does the car travel while decelerating?
Problems GROUP B
Note: Whenever necessary, use g = 9.80 m/s2. Disregard the effect of the atmosphere.
8. A ball is thrown from the ground to the top of the school flagpole. If it returns to the ground after 4.0 s, what is the height of the flagpole in meters?
Questions GROUP A
1. If a steel ball is placed on the top of a level table, it will remain there. (a) What forces are acting on the ball in this situation? (b) Are there any unbalanced forces acting on the ball?
2. (a) If the steel ball of Question 1 is given a slight push, what happens to the ball? (b) What forces act on the ball after it has been pushed? (c) Are any of these unbalanced forces? (d) What is the effect of the various forces on the motion of the ball?
3. (a) State Newton's first law of motion. (b) Describe the motion of a body in equilibrium.
4. (a) If other conditions are constant, how does the acceleration of an object vary with the amount of force applied? (b) How does the direction of the acceleration compare with the direction of the applied force?
5. How does the acceleration produced on different objects by equal forces vary with the mass of each object?
6. (a) State Newton's second law of motion. (b) What equation expresses the relationship of force to mass and acceleration?
7. How can the amount of force required to produce a certain acceleration of an object of known weight be calculated?
8. Suppose a brick is suspended from a rigid support by a suitable length of cord. (a) What downward force acts on the brick? (b) If this force is the action force, what force is the reaction force?
9. (a) What upward force acts on the suspended brick in Question-8? (b) If this force is the action force, what is the corresponding reaction force?
Questions GROUP B
10. (a) What is meant by a thought experiment? (b) Give an example.
11. Why does a falling object in a vacuum undergo constant acceleration?
12. (a) Does Newton's second law hold only when frictional forces are absent? (b) Explain.
13. A fishline will break when a force of more than 600 n is exerted on it. Two people pull on the line in opposite directions with a force of 400 n each. (a) Will the fishline break? (b) Explain.
14. Explain the thought experiment you could devise to determine the mass of an object if you had only the following objects: a frictionless horizontal plane, a l-kilogram standard, a meter stick, a spring balance in which the scale is marked in units unknown to you, and a stopwatch.
15. A tractor is pulling a heavy load. (a) If, according to Newton's third law, the load is pulling back as hard as the tractor is pulling forward, then why does the tractor move? (b) Make a drawing of the situation and show the appropriate force vectors.
16. If a third spring balance is placed between the other two in Figure 3-17 and in line with them, what will be the reading on the center balance? Test your answer in the laboratory.
Problems GROUP A p 63
Note: Use g = 9.80 m/s2. All forces are net forces.
1. What force is required to accelerate a 3.0-kg object (which is free to move) at 5.0 m/s2.
2. What is the mass of an object that is accelerated 3.00 m/s2 by a force of 125 n?
3. What acceleration does an object, mass 15 kg, undergo when a force of 25 n acts on it?
4. What is the weight of a 24-kg block of stone at sea level?
Problems GROUP B
Note: Use g = 9.80 m/s2. All forces are net forces.
5. What is the mass of a bag of cement that weighs 485 n at sea level?
6. What force is required to give a projectile weighing 475 n an acceleration of 3.00 x 103 m/s2?
7. A truck weighs 1.0 x 105 n. What force will give it an acceleration of 1.5 m/s2?
Questions GROUP A
1. (a) What force acts on an artificial satellite in orbit around the earth? (b) What force is the satellite exerting?
2. (a) On what factors does the magnitude of the force of gravitation depend? (b) How is the force of gravity related to these factors?
3. Why must we exert five times as much force to lift a mass of 5 kg as we must to lift a mass of 1 kg?
4. Assuming your mass remains constant, how will your weight vary as you go from Colorado Springs, elevation 1800m, to the top of Pikes Peak, elevation 4300 m?
5. Even though your mass remains constant, what happens to your weight as you drive from the entrance to Death Valley National Monument, elevation 1600 m, down to the lowest spot in Death Valley, 85 m below sea level?
6. Describe the method used by Cavendish to measure the universal gravitational constant.
Questions GROUP B
7. (a) How does the weight of an object vary as it is transported from the earth to the moon? (b) How would its weight vary if it were transported to the center of the earth?
8. Why does the equation g =Gme/d2 give a theoretical and not an actual value for the acceleration due to gravity at a given location?
9. (a) What is meant by a gravitational field? (b) How is gravitational field strength defined?
Problems GROUP A p 68
1. The acceleration due to gravity on the moon is 1.62 m/s2. If a person weighs 795 n on the earth, what will the person's weight be on the moon?
2. The instrument-carrying payload of a spaceship weighs 1058 n on the surface of the earth. What does it weigh 2.560 x 104 km above the earth?.
3. The acceleration due to gravity at Hartford, Connecticut, is 9.80336 m/s2. What is the force of gravitation in newtons on a mass of 0.250000 kg at this location?
Problems GROUP B
4. What is the force of gravitation between two spherical 100-kg masses whose centers are 2.00 m apart?
7. Show that the dimensions of g in the equation g = Fw/m are m/s2.
Questions GROUP A
1. (a) Give examples of forces exerted by bodies in contact with each other. (b) What types of forces do not require such contact?
2. What device is frequently used to measure forces in physics?
3. What two properties of a force are represented by a force vector?
4. (a) What is a resultant force? (b) How is the resultant found when two concurrent forces act at an angle of Oo or 180o ?
5. How is the resultant of two concurrent forces found that act at right angles to each other?
6. What is the first condition of equilibrium?
7. (a) What is an equilibrant force? (b) At what point must it be applied? (c) How does it compare with the resultant force?
8. What is the relationship between the first condition of equilibrium and Newton's first law of motion?
9. How is the resultant of two concurrent forces found that act at an angle to each other that is not a right angle?
Problems GROUP A p 75
Note: Solve the following problems: (a) graphically and (b) Trigonometrically:
1. Two forces act simultaneously on point A. One force is 5.0 n south; the other is 15.0 n south. Determine the magnitude and direction of the resultant force vector.
2. Two forces act on point E. One is 20.0 n north; the other is 20.0 n 30.0o south of east. Find the magnitude and direction of (a) the resultant, (b) the equilibrant.
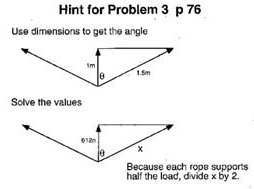
3. A person weighs 612 n. If the person sits in the middle of a hammock that is 3.0 m long and sags 1.0 m below the points of support, what force would be exerted by each of the two hammock ropes. (Hints: Get the angle using distances, then solve for x using forces. Remember each rope gets half the load). See Hint below.

Questions GROUP A
1. How is the resolution of forces related to the composition of forces?
2. What is the angle between the components into which a force vector is usually resolved?
3. What is meant by a normal force?
4. A car is parked on a hill. (a) Into what two convenient components can the weight of the car be resolved? (b) Which component is counteracted by the brakes of the car?
Questions GROUP B
5. (a) Describe two convenient components of the weight of an object lying on an inclined plane. (b) How are the magnitudes of these components related to the angle of the incline?
6. The transmitting tower of a TV station is held upright by guy wires that extend from the top of the tower to the ground. The wires make a 30.0o angle with the tower. Into what two components can the force that the tower exerts on each guy wire be resolved?
Problems GROUP A p 78
Note: Solve the following problems (a) graphically and (b) trigonometrically:
1. A person pushes with 150.0 n of force along the handle of a lawn roller. The angle between the handle and the ground is 45.0o. Determine the magnitudes of the horizontal and vertical components of this force.
2. A truck weighing 1.00 x 105 n is parked on a hill that rises 3.00 m in each 100 m of road. What is the magnitude of the component of its weight that tends to make the truck roll down the hill? (Hint: Use proportional triangles. See hint below).
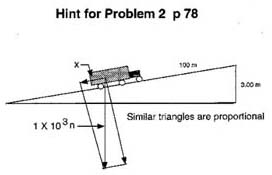
3. A force of 25.0 n acts on point C at an angle of 35.0o west of north. What are the magnitudes of the northward and westward components of this force?
4. A person pulls a sled along level ground. The rope with which the person pulls the sled makes an angle of 20.0" with the ground as the person pulls with a force of 78.0 n. What are the horizontal and vertical components of the force?
Problems GROUP B
Note: Solve the following problems (a) graphically and (b) trigonometrically.
6. A sign weighing 495 n is supported as shown in Figure 4-12. Determine the magnitudes and directions of the forces exerted by the chain and by the bracket. Assume that the horizontal rod cannot support vertical forces.
7. A block of stone having a mass of 2.00 x 103 kg is to be raised by a crane. The angle between the load cable and the crane boom is 30.0o. The hinged boom is held in place by a tie cable that forms an angle of 20.0o with the boom. (See Figure 4-13.) Determine the magnitude of the thrust force (pull) of the cable.
8. The rafters of a roof meet at a 120o angle. What force is exerted along the rafters by an object weighing 6.00 x 103 n suspended from the peak?
Questions GROUP A
1. (a) What is friction? (b) What ideas have scientists presented to explain friction?
2. Give several examples of ways in which friction is helpful.
3. What methods are used to reduce friction?
4. How does sliding friction compare with starting friction?
5. (a) On what does the amount of sliding friction usually depend? (b) Of what is it independent?
6. What is meant by the coefficient of friction?
Questions GROUP B
7. What is the direction of the force of friction when two surfaces are moving over one another?
8. Name several devices that increase friction between the tires of a car and the pavement.
9. Why does a lubricant reduce friction in a bearing?
10. (a) Under what conditions is the weight of an object the same as the normal force pressing it to the surface over which it is moving? (b) How is the normal force component of the weight of an object determined under other conditions?
Problems GROUP A p 85
Note: For each problem, draw a force diagram using a suitable scale, and then perform the necessary calculations.
1. A block weighs 2.00 x 103 n. If a horizontal force of 1.00 x 102 n is required to keep it in motion with constant speed on a horizontal surface, what is the coefficient of sliding friction?
2. In a coefficient of friction experiment, a horizontal force of 45 n was needed to keep an object weighing 125 n sliding at constant speed over a horizontal surface. Calculate the coefficient of sliding friction.
3. A crate weighing 1.25 x 103 n slides down an inclined plane at constant speed. The plane is 6.0 m long. Its height is 3.0 m. What is the coefficient of sliding friction between the crate and the inclined plane?
Problems GROUP B
4. The coefficient of sliding friction between a metal block and the inclined surface over which it will slide is 0.200. If the surface makes an angle of 20.0o with the horizontal and the block has a mass of 80.0 kg, what force is required to slide the block at constant speed up the plane?
Questions GROUP A
1. Define center of gravity.
2. (a) What are parallel forces? (b) How is the resultant of two parallel forces that act in the same direction calculated? (c) How is the resultant of parallel forces that act in opposite directions calculated?
3. Explain how two persons of unequal weight can be made to balance on a seesaw.
4. (a) A force acts at right angles to a pivoted bar. How is the torque produced by this force calculated? (b) What is the unit of torque?
5. If a bar on which parallel forces act is to be in equilibrium, what conditions must be met?
Questions GROUP B
6. How can the choice of the pivot point simplify the calculations of the torques in a problem?
7. Distinguish between center of gravity and the pivot point.
8. Give an example of an object with a center of gravity that is not within the object.
9. A certain force does not act at right angles to a pivoted bar. How is the torque from this force calculated?
10. (a) What is a couple? (b) How is the torque of a couple calculated',
Problems GROUP A p 90
Note: For each problem, draw a force diagram using a suitable scale and perform the necessary calculations. Unless otherwise noted, the center of gravity is at the geometric center of the object.
1. A steel beam of uniform cross section weighs 2.5 x 105 n. If it is 5.00 m long, what force is needed to lift one end of it?
2. A bar 4.0 m long weighs 400 n. Its center of gravity is 1.5 m from one end. A weight of 300 n is attached at the heavy end and a weight of 500 n is attached at the light end. What are the magnitude, direction, and point of application of the force needed to achieve translational and rotational equilibrium of the bar?
3. A painter weighing 875 n stands on a plank 3.00 m long, which is supported at each end by a stepladder. The plank weighs 223 n. If the painter stands 1.00 m from one end of the plank, what force is exerted by each stepladder?
4. A bricklayer weighing 8.00 x 102 n stands 1.00 m from one end of a scaffold 3.00 m long. The scaffold weighs 750 n. A pile of bricks weighing 3.20 x 102 n is 1.50 m from the other end of the scaffold. What force must be exerted on each end of the scaffold. What force must be exerted on each end of the scaffold in order to support it?
7. The bridge AB in Figure 4-29 is 36.5 m long. It weighs 2.56 x 105 n. A truck weighing 5.25 x 104 n is 10.2 m from one end of the bridge. Calculate the upward force that must be exerted by each pier to support this weight.
Questions GROUP A
1. How is motion along a curved path produced?
2. (a) A projectile is fired horizontally. What motions can be used to explain its path? (b) What effect does each of these motions have on the path of the projectile?
3. (a) What is uniform circular motion? (b) What force causes circular motion? (c) Why must a force be used to produce circular motion?
4. What factors determine the magnitude of a centripetal force?
5. (a) How does motion in a vertical circle differ from uniform circular motion? (b) What causes this difference? 6. (a) What is meant by critical velocity? (b) What happens to an object that does not have critical velocity? 7. (a) What is meant by a frame of reference? (b) List the four frames of reference that could be used to describe the motion of an earth satellite.
Questions GROUP B
8. (a) What adjustment is made on the rear sight of a rifle when the distance to the target is increased? (b) How would the use of a higher velocity bullet affect the adjustment?
9. Why does an astronaut experience large forces (a) during the launching of a space vehicle? (b) during the reentry of the vehicle?
10. (a) In what way is the motion of a satellite in a circular orbit similar to motion in a vertical circle? (b) How are the two motions different?
11. Evaluate the statements: (a) "An earth satellite is weightless." (b) ''An earth satellite is continuously falling around the earth."
12. Describe the motion of a person on a merry-go-round in terms of two different frames of reference.
Problems GROUP A p 101
1. What is the centripetal acceleration of an object moving along a horizontal circular path of 16.0 m radius with a speed of 40.0 m/s ?
2. If the mass of the object in Problem 1 is 2.00 metric tons (a metric ton = 1000 kg), what centripetal force is required to maintain it in a circular path?
3. A ball of mass 2.5 x 10-2 kg is swung at the end of a string in a horizontal circular path at a speed of 5.0 m/s. If the length of the string is 2.0 m, what centripetal force does the string exert on the ball?
4. Calculate the centripetal force exerted on a 5.0-kg mass that is moving at a speed of 3.0 m/s in g horizontal circular motion if the radius of the circle is (a) 1.0 m; (b) 3.0 m.
Problems GROUP B
6. An automobile weighs 6.0 x 104 n. If it is driven around a horizontal curve that has a radius of 250 m at the rate of 22 m/s, what is the centripetal force of the road on the automobile?
7. What is the orbiting speed of a satellite moving uniformly in a circular path 1.00 x 103 km above the earth? Hint: find g first by inverse square proportion.
Questions GROUP A
1. (a) What is rotary motion? (b) Give examples of uniform and variable rotary motion.
2. What is a radian?
3. (a) What is angular velocity? (b) What is angular acceleration? 4. (a) Explain why angular velocity is a vector quantity. (b) How is a vector representing an angular velocity drawn?
5. How do equations for uniformly accelerated rotary motions compare with those for uniformly accelerated linear motions?
Questions GROUP B
6. Explain how a spinning flywheel maintains the shaft on which it is mounted at a constant angular velocity.
7. What is the result of the addition of two angular velocities about different axes?
8. For a rotating wheel, how do the directions of the linear velocity vector and the angular velocity vector compare at the same instant of time?
9. In the case of precession, how do the directions of an angular acceleration vector and the corresponding angular velocity vector compare? See Figure 5-13 below.
10.(a) What causes precession? (b) How does precession affect the position of the North Star?

Problems GROUP A p 108
1. What is the angular velocity in radians per second of a flywheel spinning at the rate of 4820 revolutions per minute?
2. If a wheel spins at a rate of 625 rad/s, what is its angular velocity in revolutions per minute?
3. A net force of 10.0 n is applied tangentially to the rim of a wheel having a 0.25 m radius. If the rotational inertia of the wheel is 0.500 kg m2, what is its angular acceleration? Hint: a = Fr / l.
4. Calculate the rotational inertia of a thin ring whose mass is 5.7 kg and whose radius is 0.15 m and that rotates about an axis through the center perpendicular to the plane of the ring.
5. What is the rotational inertia of a solid ball 0.050 m in radius that weighs 80.0 n if it is rotated about a diameter?
Problems GROUP B
6. Calculate the angular acceleration in radians per second2 of a wheel that starts from rest and attains an angular velocity of 545 revolutions per minute in 1.00 minute. Hint: 1 rev = 2 p radians.
Questions GROUP A
1. How is periodic motion related to simple harmonic motion?
2. Define the following terms as they apply to simple harmonic motion: (a) complete vibration; (b) displacement; (C) period; (d) frequency. 3. What factors determine the period of a pendulum?
4. (a) What is a physical pendulum? (b) How is it related to a simple pendulum?
5. Describe two ways of finding the center of percussion of a baseball bat.
Questions GROUP B
6. (a) If a pendulum clock loses time, should the pendulum be made shorter or longer? (b) Explain.
7. Describe a method of using the simple pendulum to find the value of g for a given location.
8. Explain why less net force is exerted on the mass in Figure 5-15, below, as the mass returns to its equilibrium position.
9. (a) In what sense may the balance wheel of a wrist watch be compared with a simple pendulum? b) Relate the vibration of the quartz crystal in some wrist watches to the simple pendulum.
Problems GROUP A p 113
1. A pendulum 0.25 m long has a period of 1.1 s. What is the period of a pendulum in the same location if it has a length of 0.10 m?
2. What is the period of a pendulum 1.5 m long at sea level?
Problems GROUP B
3. What is the value of g for a location where a pendulum 1.08 m long has a period of 2.05 s ?
Questions GROUP A
1. Give the scientific definition of "work."
2. (a) How is a graph used to find the work done by a varying force? (b) What method for finding the work done can easily be applied if the force varies constantly?
3. Is work done by the centripetal force that produces circular motion? Explain.
4. (a) List the six simple machines. (b) Into what two basic types can they be divided?
5. (a) Define efficiency for a machine. (b) How is it computed?
6. How does friction affect the efficiency of machines?
7. List the advantages and disadvantages of friction in the use of a screw.
8. a) Give the scientific definition of power. b) What is the SI unit of power?
Questions GROUP B
9. How are the coordinates of a graph used to find the area under a given curve?
10. Suppose that you have two simple machines, each of which multiplies a force by a factor of three. By what factor will the force be multiplied if the two machines are used in series? Explain.
11. (a) What physical quantity is expressed in kilowatt-hours? (b) Use dimensional analysis to verify your answer.
12. Show how the formula for power in rotary motion is derived.
Problems GROUP A p 123
1. A person weighing 750 n climbs a flight of stairs that is 5.0 m high. What work does the person do?
2. What work is done when a person lifts a 2.5-kg package and places it on a shelf 2.2 m high?
3. How much work must be done to roll a metal safe, mass 116 kg, a distance of 15.0 m across a level floor? The coefficient of friction is 0.050.
4. A sled is pulled over level snow a distance of 0.500 km by a force of 124 n applied to a rope that makes an angle of 35.0owith the snow. How much work is done?
5. A force of 18 n is required to stretch a spring 0.25 m from its equilibrium position. (a) Compute the amount of work done on the spring. (b) How much force is required to stretch the spring 0.50 m (assuming that the elastic limit of the spring is not exceeded)? (c) Compute the amount of work done. Hint: W=1/2FDd.
6. A force of 545 n is exerted on the rope of a pulley system, and the rope is pulled in 10.0 m. This work causes an object weighing 2520 n to be raised 1.50 m. What is the efficiency of this machine?
7. Two people use a wheel and axle to raise a mass of 750 kg. The radius of the wheel is 0.50 m, and the radius of the axle is 0.040 m. If the efficiency of the machine is 62% and each person exerts an equal force, how much force must each apply?
8. The raised end of an inclined plane 4.0 m long is 0.90 m high. Neglecting friction, what force is required to push a steel box weighing 750 n up this plane?
9. A jackscrew has a lever arm 0.75 m long. The screw has 1.5 threads to the centimeter. If 320 n of force must be exerted in order to raise a load of 6.0 x 103 kg, calculate the efficiency.
10. What power is required to raise a mass of 47 kg to a height of 12 m in 15 s?
11. A loaded elevator has a mass of 2.50 x 103 kg. If it is raised in 10.0 s to a height of 50.0 m, how many kilowatts are required?
12. The mass of a large steel ball is 1500 kg. What power is used in raising it to a height of 33 m if the work is performed in 30.0 s?
Questions GROUP A
1. Differentiate between (a) potential and kinetic energy; (b) gravitational potential energy and elastic potential energy.
2. Show how the formula for gravitational potential energy is derived from the work formula.
3. (a) Describe the kinetic energy of the wheel of a moving automobile. (b) Give the equations that can be used to calculate this energy.
4. (a) What determines the force required to stretch or compress a spring? (b) In what units is this factor expressed?
5. (a) Define mechanical energy. (b) How is it conserved in pendular motion?
Questions GROUP B
6. (a) Show how the equation for kinetic energy is derived. (b) Use analysis to show that kinetic energy expressed in work units.
7. (a) Distinguish between conservative and dissipative forces. (b) Why is force of friction a dissipative force?
8. Describe the forms of energy in the two parts of Figure 6-13.
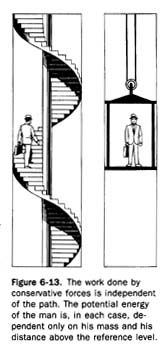
Problems GROUP A p 130
1. A mass of 2.00 kg is lifted from the floor to a table 0.80 m high. Using the floor as a reference level, what potential energy does the mass have because of this change of position?
2. A large rock with a weight of 1470 n rests at the top of a cliff 40.0 m high. What potential energy does it have using the bottom of the cliff as a reference level?
3. What is the kinetic energy of a baseball having a mass of 0.14 kg that is thrown with a speed of 18 m/s?
4. A meteorite weighing 1860 n strikes the earth with a velocity of 45.2 m/s. What is its kinetic energy?
6. The force constant of a spring is 150 n/m. (a) How much force is required to stretch the spring 0.25 m? (b) How much work is done on the spring in that case?
Problems GROUP B
9. What is the kinetic energy, in joules, of an electron that has a mass 9.1 x 10-3 kg and that moves at a speed of 1.0 x 107 m/s? The rotor of an electric motor has a rotational inertia of 45 kg m2. What is its kinetic energy if it turns at 1500 revolutions per minute?
Questions GROUP A
1. (a) What is impulse? (b) What is momentum? (c) How are impulse and change of momentum related.
2. Why do both a slowly docking ferryboat and a speeding rifle bullet have a large amount of momentum?
3. Are impulse and momentum scalar or vector quantities?
4. What is the law of conservation of momentum?
5. How does an aerial display of fireworks illustrate conservation of momentum?
6, Distinguish between elastic and inelastic collisions.
7. What is meant by an isolated system? Consider torques as well as forces in your answer.
8. Give examples of one-dimensional and two-dimensional collisions.
9. Explain why it is impossible for a moving ocean liner or a speeding airplane to make an abrupt turn.
10. What happens to the momentum of a car when it stops?
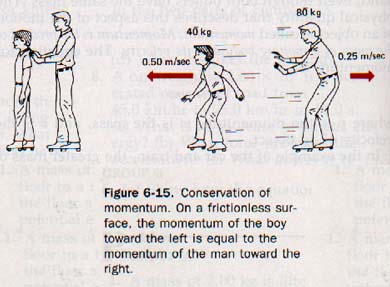
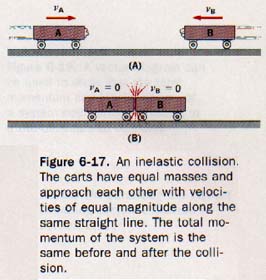
Fig 6-15 Fig 6-17
Problems GROUP A p 138
1. A 508-kg mass is at rest and is free to move. At a certain time, 25.0 s after a force acts on it, the mass has a velocity in the direction of the force of 150 m/s. What is the magnitude of the force?
2. A bullet, mass 60.0 g, is fired from a that is suspended by wires and is to move. The mass of the gun is 5.00 kg. The speed of the bullet is 615 m/s. What is the speed of recoil of the gun?
3. A 1.50-kg ball whose velocity is 8.00 m/s southward collides with a 2.00-kg ball traveling along the same path with a velocity of 3.00 m/s southward. If the velocity of the 2.00-kg ball is 7.29 m/s southward after impact, what is the velocity of the 1.50-kg ball?

Questions GROUP A
1. List the basic concepts of the kinetic theory.
2. (a) What is meant by the phase of matter? (b) Describe the three phases of matter.
3. Distinguish between a molecule and an atom.
4. Under what circumstances are the forces between molecules in a solid (a) attractive (b) repulsive
5. (a) What are the two classes of solids? (b) What is the particle arrangement in each?
6. (a) Describe the motion of the particles of a solid. (b) What experimental evidence supports this description?
7. What name is given to the force of attraction between (a) like molecules, (b) unlike molecules?
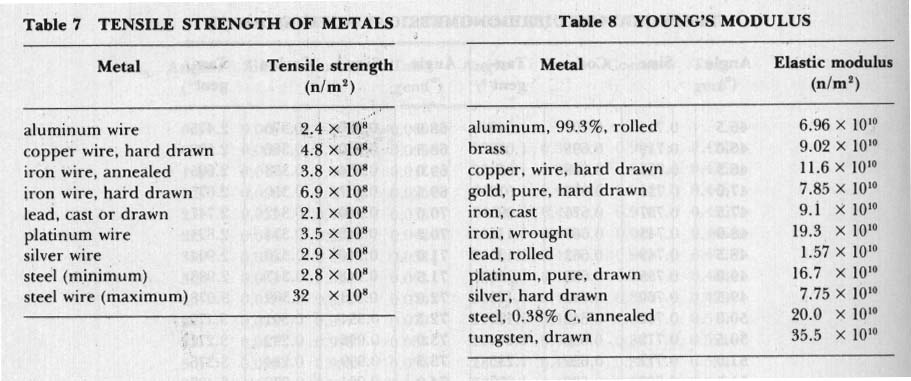
8. (a) What is tensile strength? (b) In what units is the value for tensile strength expressed?
9. Define elasticity.
10. Distinguish between stress and strain.
11. What is meant by the elastic limit?
12. State Hooke's law.
13. Give the equation for Young's Modulus and identify each of its terms.
Questions GROUP B
14. For a given mass of matter that can exist as a solid, a liquid, and a gas, what does the volume indicate the spacing between molecules in these three phases?
15. (a) What is the magnitude of an atomic mass unit? (b) How is this value established?
16. What direct evidence is there that matter is composed of molecules?
17. What happens to the crystal pattern of an elastic material when its limit is exceeded?
18. What is the relationship between Hooke's law and the force (Section 6.10)?
Problems GROUP A p 150
1. A coiled spring is stretched 0.050 m by a mass weighing 0.500 n that is hung from one end. How far will it be stretched by a mass weighing 1.000 n?
2. The hook of a spring balance is pulled down 5.00 cm by a mass weighing 40.0 n. (a) If a mass weighing 125.0 n is substituted for the previous mass, how far is the hook pulled down? (b) How far apart are the 5.00-n graduations on the scale? Hint: 5cm / 40n X 5n = 0.625 cm/n.
3. Two identical wires are 125.0 cm 375.0 cm long. The first wire is broken by a force of 489.0 n. What force is needed to break the other?
4. A copper wire 100.0 cm long 0.200 cm in diameter is suspended from a solid support. A 10.00-kg mass is hung from the lower end of the wire. (a) Determine the stress in wire. (b) Determine the strain in wire. Hints: 1 m2 = 104 cm2 . 1 kg = 9.8 n. See Table 8.
5. The cross-sectional area of an aluminum wire is 2.50 x 10-3 cm2 force will break it?
Questions GROUP A
1. What property of liquid molecules did Brown's experiment show?
2. Describe a demonstration that shows that molecules of liquids diffuse.
3. (a) In terms of adhesion and cohesion, explain why alcohol clings to a glass rod and mercury does not. (b) What is the relationship between cohesion and viscosity?
4. What is the effect of adding a detergent to the water on which a needle is supported?
5. Why is a soap bubble floating through the air spherical in shape?
6. What determines whether a meniscus is concave or convex when viewed from above?
7. Water rises to a certain height in a capillary tube of given diameter. What is the effect on the amount of rise if (a) the tube is lengthened, (b) the diameter of the tube is decreased, (c) the temperature of the water is raised?
8. (a) Which change of phase is called melting? (b) What name is given to the temperature at which melting occurs? (c) What is freezing? (d) What name is given to the temperature at which freezing occurs?
9. (a) Which has a greater density, water or ice? (b) Explain in terms of molecular arrangement. 10. What is the meaning of the term "regelation" ?
11. In terms of the kinetic theory, explain why gases (a) expand when heated, (b) exert pressure, (c) diffuse porous substances.
Questions GROUP B
l2. Describe the Properties of the particles of a substance that is liquid at room temperature.
13. Describe the forces that are acting when a razor blade is supported on water.
14. Why is lead shot made by allowing melted lead to fall through cool air?
l5. In terms of adhesion and cohesion, explain why mercury is depressed in capillary tubes.
16. Describe the forces that cause water to rise in a capillary tube.
17. Why do crystalline solids have a definite melting point and noncrystalline solids do not?
18. What is the effect of increased pressure on the freezing point of (a) substances that contract as they freeze, substances that expand as they freeze?
19. Why is it easier to skate with sharp ice skates than with dull ones?
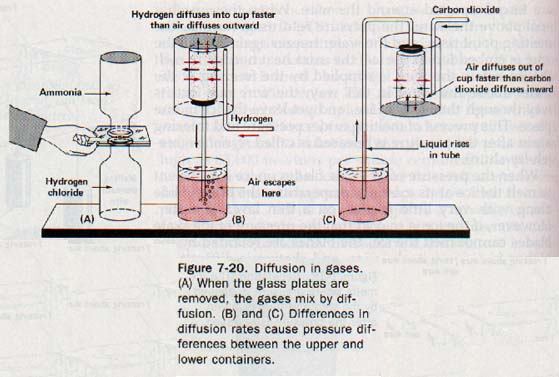
20. What would happen if the gas introduced into the large beaker of the apparatus shown in Figure 7-20B (see below) were (a) helium, (b) argon?
21. (a) What is plasma? (b) Why is most of the matter in the universe in the form of plasma?
Questions GROUP A
1. Distinguish between thermal energy and heat.
2. How do heat and temperature differ? Why were the temperature of the melting point of ice and the temperature of the boiling point of water originally called "fixed points" in defining a temperature scale?
3. What single fixed point is now used for the definition of temperature scales?
5. Compare the magnitude of a Celsius degree with that of a Kelvin degree.
6. (a) What is the Celsius temperature at absolute zero? (b) What would be the thermal energy of a material at absolute zero?
7. Compare the amount of thermal energy possessed by each of the following: (a) a soldering iron and a needle, both at 150 oC; (b) a 4-section radiator and a I0-section radiator; (c) a kettle of boiling water and cup of boiling water; (d) 20.0 kg of ice at -10.0 oC and 10.0 kg of ice at -10.0 oC (e) a liter of liquid air and a milliliter of liquid air, both at -189 oC.
8. How are quantities of heat measured?
9. What is a kilocalorie?
Questions GROUP B
10. How does the thermal energy of a material determine its temperature?
Problems GROUP A p 171
1. The temperature in a classroom is 24.0 oC. What is the Kelvin reading?
2. Liquid nitrogen boils at 77.0 oK. What is the reading on the Celsius scale?
3. The boiling point of liquid oxygen is -183 oC. What is this temperature in oK?.
4. What is the boiling point of helium on the Celsius scale if its boiling point is 4.1 oK?
5. How many calories will be needed to change the temperature of 500 g of water from 20 oC to 100 oC?
Questions GROUP A
1. What is meant by the coefficient of linear expansion?
2. What provision is made to allow for the expansion of (a) concrete highways, (b) bridges, (c) piston rings?
3. A hole 1.00 cm in diameter is drilled through a piece of steel at 20.0 oC. What happens to the diameter of the hole as the steel is heated to 100.0 oC? Hint: think of all of the molecules pushing each other further apart.
4. A platinum wire can be easily sealed into a glass tube, but a copper wire does not form a tight seal with glass. Explain.
5. How does the coefficient of volume expansion of mercury compare with the coefficient of volume expansion of glass?
6. Why are mercury and alcohol used in making thermometers?
7. Why does the pressure of a confined gas increase as its temperature is raised?
8. What is the meaning of STP?
9. (a) What is a mole? (b) How is the mole related to Avogadro's number?
10. How does the density of a gas vary with the pressure exerted on it?
Questions GROUP B
11. Does the coefficient of linear expansion depend on the unit of length used? Explain.
12. Why do solids expand when their temperature is raised?
13. (a) Why does water contract as its temperature is raised from O oC to 4 oC? (b) Why does it expand when heated above 4 oC?
14. Why does the measurement of the expansion of a liquid contained in a bulb or tube fail to give a true value for the expansion of the liquid?
15. A brass disk fits a hole in a steel plate snugly at 20.0 oC. In order to make the disk drop out of the plate, should the disk and plate combination be heated or cooled? Hint: think of all of the molecules pushing each other further apart.
16. Why are the coefficients of volume expansion very nearly equal for all gases?
17. Why do real gases within the usual experimental ranges of temperature and pressure conform to the behavior of an ideal gas?
Problems GROUP A p 181
1. A piece of copper pipe is 5.00 m long at 20.0 oC. If it is heated to 70.0 oC, what is the increase in its length?
2. A rod of silver is 100.0 cm long at 0.0oC. What is its increase in length when heated to 100.0 oC?
3. A steel pipeline is 1500 m long at 30.0 oC. What is its length when the temperature is 10.0 oC?
5. A quantity of carbon tetrachloride occupies a volume of 500.00 mL at 20.0 oC. What is its volume at 45.0 oC? Hint: D = M / V .
6. The gasoline in the underground storage tanks of a service station is at a temperature of 15.0 oC. What is the volume of 125.0 L of the gasoline after it warms up to 25.0oC in the fuel tank of a car?
8. A gas occupies 2.00 L at 73.5 mm pressure. What is the volume at standard pressure if the temperature is unchanged? Hint: The Gas Laws-- PV / T = P'V' / T' . Std Press = 760 mm.
7. A gas occupies a volume of 250.0 cm3 at 37 oC. What is its volume at 67 oC if the pressure is not changed?
10. A certain gas has a density of 1.55 g/L at a pressure of 760 mm. What is the density if the pressure is decreased to 725 mm? Hint: D = M / V .
Questions GROUP A
1. What is the heat capacity of a body?
2. (a) Give a word definition for specific heat. (b) What is the formula that defines specific heat?
3. How do the specific heats of most common substances compare with the specific heat of water?
4. How is the amount of thermal energy required to produce a given temperature change in a substance calculated?
5. What is the law of heat exchange?
6. What data are required for the determination of specific heat by the method of mixtures?
7. On what basic law are experiments with calorimeters based?
Problems GROUP A p 187
Hint: Heat Lost = Heat Gained, Q = Q, so mcDt = mcDt. See Sample Probs and Sample Mixture problems in your text or notes.
1. How much heat is given out when 85 g of lead cools from 200 oC to 10 oC?
2. If 10.0 g of water at 0.0 oC is mixed with 20.0 g of water at 30.0 oC, what is the final temperature of the mixture?
3. What is the final temperature of a mixture of 135 g of water at 21.0 oC in a 45.0 g brass calorimeter and 200 g of silver at 100.0 oC?
4. A piece of tin weighing 225 g and having a temperature of 100.0 oC is dropped into 10.0 g of water at a temperature of 10.0 oC. If the final temperature of the mixture is 20.0 oC, what is the specific heat of the sample of tin? Hint: Heat Lost = Heat Gained, Q = mcDt
Questions GROUP A
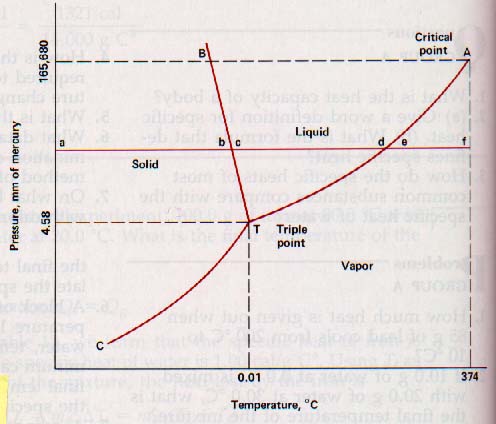
1. Draw the temperature-pressure equilibrium curves for water.
2. (a) What is heat of fusion? (b) What is the value for the heat of fusion of ice?
3. What is supercooling?
4. For what purposes are (a) pressure cookers, (b) vacuum pans used?
5. Explain the processes of (a) distillation, (b) fractional distillation.
6. (a) What is heat of vaporization? (b) What is the magnitude of heat of vaporization of water?
7. Why does steam at 100 oC produce a more severe burn to the skin than the same mass of water at 100 oC?
8. What is meant by the critical point?
9. The air above the ice of a pond is -10 oC. What is the probable temperature of (a) the upper surface of the ice; (b) the lower surface; (c) the water just beneath the surface; (d) the water at the bottom of the pond?
Questions GROUP B
14. (a) Why does the boiling temperature of a liquid depend on the pressure exerted on its surface? (b) How does the boiling temperature of a liquid vary with the pressure exerted on its surface?
15. How can fractional distillation be used in separating the different liquids in petroleum?
16. What data are required in order to determine the heat of vaporization of water by the method of mixtures? Why does the heat of vaporization vary with the boiling temperature?
17. Why does the heat of vaporization vary with the boiling temperature?
Problems GROUP A p 197
1. How many calories will be absorbed by 1.50 kg of ice at 0.0 oC as it melts?
2. To what temperature must a 2270 g iron ball be heated so that it can completely melt 1150 g of ice at 0.0 oC?
3. A 500 g aluminum block is heated to 350 oC. How many grams of ice at 0.0 oC will the aluminum block melt on cooling?
6. How many calories are given off by 50.0 g of steam at 100 oC when it condenses?
7. How many calories are used to vaporize 20.0 kg of water at 100 oC?
8. Calculate the number of calories evolved when 4.00 kg of steam at 100 oC is condensed, cooled, and changed to ice at O oC.
Questions GROUP A
1. What is thermodynamics?
2. State the first law of thermodynamics. What is the meaning of the term mechanical equivalent of heat?
3. What is the metric value for the mechanical equivalent of heat?
5. What is (a) an isothermal process, (b) an adiabatic process?
6. Give an example of (a) an isothermal expansion, (b) an adiabatic expansion.
7. How does the specific heat of gases differ from that of a solid or liquid?
8. Define two kinds of specific heat for a gas.
Questions GROUP B
9. How does the first law of thermodynamics differ from the mechanical conservation of energy principle?
10. Describe Joule's method for determining the mechanical equivalent of heat.
11. What physical law governs the isothermal expansion and compression of an ideal gas?
12. What physical laws govern the adiabatic expansion and compression of an ideal gas?
l3. (a) What is the source of the heat equivalent of the work done by an ideal gas during isothermal expansion? (b) What happens to the heat equivalent of the work done on an ideal gas during isothermal compression?
14. (a) What is the source of the heat equivalent of the work done by an ideal gas during adiabatic expansion? (b) What happens to the heat equivalent of the work done on an ideal gas during adiabatic compression?
15. When an ideal gas expands isothermally, it does work on its surroundings. Does the energy of the gas change during this process? (b) What is the source of the energy by which the gas can do this work?
16. (a) Does a gas do work on its surroundings when the gas expands adiabatically? (b) What is the source of energy by which the gas can do this work?
Problems GROUP A p 206
1. How many joules can ideally be obtained from 1.00 x 104 cal?
2. Gasoline, mass density 0.700 g/cm3, liberates 1.15 x 104 cal/g when it is burned. How many joules of work can be obtained by burning 1.00 L of gasoline?
3. The water going over Niagara Falls drops 50.6 m. How much warmer is the water at the bottom of the falls than it is at the top? Disregard any possible effects of evaporation of water during the fall. Hint: Assume a 1 Kg mass of water. For Q = mcDt, m is in grams (assume 1000g) and for PE = mgh, m is in kg (assume 1 kg). To change PE (in joules) to calories, use 1 cal = 4.18 j, so 1 j = 1 / 4.18 cal).
Problems GROUP B
4. The natural gas burned in a gas turbine has a heating value of 1.00 x 105 cal/g. If 2.00 g of gas are burned in the turbine each second and the efficiency of the turbine is 25.0%, what is the output in kilowatts? Hint: P = w / t, 1 cal = 4.18 j, 1 kw = 1000 w.
5. How much heat will be produced if a 1.25-kg mass moving at 26.6 m/s strikes a wall and all the energy is converted to heat? Hint: Q = Ek = 1/2mv2, 1 cal = 4.19 j.
Questions GROUP A
1. What is the purpose of (a) a heat source, (b) a heat sink?
2. On what does the efficiency of an ideal heat engine depend?
3. State the second law of thermodynamics .
4. Give two definitions of entropy.
5. Distinguish between an external combustion engine and an internal combustion engine.
6. Describe Hero's aeolipile.
7. Define the metric unit of pressure.
8. List two uses for steam turbines.
9. What factors determine the power of a gasoline engine?
10. What is meant by turbocharging?
11. How is the air-fuel mixture ignited in (a) a gasoline engine, (b) a diesel engine?
12. Describe two difficulties in developing a practical gas turbine automobile engine.
13. What is the main difference between a ramjet and a turbojet engine?
14. What is the main difference between a jet engine and a rocket?
15. (a) Define specific impulse. (b) Use dimensional analysis to show that specific impulse is measured in seconds.
16. How can heat be made to flow from a body at a low temperature to a body at a higher temperature?
17. (a) Describe two uses for a heat pump. (b) What makes a heat pump more efficient than an electric heater?
Problems GROUP B p 220
1. What is the theoretically highest efficiency of a steam engine that has a steam input temperature of 200.0 oC and a steam exhaust temperature of 100.0 oC? Hint: use oK, K = oC + 273o.
2. Referring to Problem 1, assume the temperature of the heat sink to remain at 100.0 oC. What input temperature would be required to increase the efficiency of this engine to 30.0%?
3. A 50-g ice cube melts in a beaker containing 400 g of water. The temperature of both is O oC. Calculate (a) the entropy of the ice, (b) the entropy of the water, (c) the entropy of the universe. Hint: Q = m(ice)Lf. Lf = 80 cal.g
Here Endeth the Portfolio Assignments for the First Semester