The Heat is ON

The Heat is ON

The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).
This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.
HEAT MEASUREMENTS
8.01 Relationship Between Heat and Temperature Suppose we fill a large beaker and a small beaker with boiling water. The water in the two beakers is at the same temperature, but the water in the large beaker can give off more heat. It could, for example, melt more ice than could the water in the small beaker.
It is possible, therefore, for a body to be at a high temperature and give off little heat; to be at a high temperature and give off a large quantity of heat; to be at a low temperature and give off little heat; or to be at a low temperature and give off a large quantity of heat.
When a material is hot, it has more thermal energy than when it is cold. Thermal energy is the total potential and kinetic energy associated with the random motion and arrangements of the particles of a material.
Temperature is the "hotness" or "coldness" of a material. The quantity of thermal energy in a body affects its temperature. The same quantity of thermal energy present in different bodies, however, does not give each the same temperature. The ratio between temperature and thermal energy is different for different materials.
We saw in Chapter 7 that the temperature of a substance will rise if the average kinetic energy of its particles is increased. If the average kinetic energy is decreased, the temperature goes down. On the other hand, when the potential energy of the particles is increased or decreased without a change in the average kinetic energy, a change of phase takes place without a change in temperature.
Heat is thermal energy that is absorbed, given up, or transferred from one body to another. The temperature of a body is a measure of its ability to give up heat to or absorb heat from another body. Thus, the temperature of a body determines whether or not heat will be transferred to or from any nearby body.
The experiments of Count Rumford and James Prescott Joule (Section 1.13) show that mechanical energy and heat are equivalent and that heat must be a form of energy. Since thermal energy is also defined as a form of energy, you may wonder why two different terms-- thermal energy and heat-- are used.
An example will illustrate the difference. The temperature of the air in a bicycle tire will rise when the tire is being pumped up. It will also rise when the tire is out in the sun. In both cases the thermal energy and the temperature of the air are increased. In the first case the work done in pumping was converted to thermal energy. In the second case the rise in temperature was due to energy transferred from the sun to the tire. The term heat is used when the transfer of thermal energy from one body to another body at a different temperature is involved.
Temperature is defined in terms of measurements made with thermometers that will be described later. But the following qualitative definition gives the relationship between temperature and energy. Temperature is a physical quantity that is proportional to the average kinetic energy of translation of particles in matter.
8.2 Temperature Scales The Celsius temperature scale is often heard during weather reports. In Section 7.21, we used the oC in the calculation of relative humidity. Now we will see how the Celsius scale was developed. To measure temperature it is necessary to introduce a fourth fundamental unit. The unit of temperature difference, the degree, cannot be derived from length, mass, and time; a measurable physical property that changes with temperature must be used.
There are many physical properties that change with temperature. The length of a solid, the volume of a liquid, the pressure of a gas held at constant volume, the volume of a gas held at constant pressure, and the color of a solid heated to a high temperature are examples. Some of these properties of matter can be used in developing a temperature scale and constructing a thermometer.
To establish a temperature scale it is necessary to find a process that occurs without a change in temperature. The temperature at which such a process takes place can be used as a fixed point on a temperature scale. A change of phase of a substance, such as melting or boiling, can used. The temperature at which the solid phase of a substance is in thermal equilibrium with its liquid phase as a fixed value at a given pressure. This is the melting point. The boiling point of the substance is always higher than the melting temperature.
There is only one pressure at which the solid, and vapor phases of a substance can be in contact and thermal equilibrium. This equilibrium occurs at only one temperature, which is known as the triple-point.
For example, there is only one pressure and temperature condition at which ice, liquid water, and water can exist in a vessel in thermal equilibrium. The ice, water, and vapor are all at the same temperature and continue to exist indefinitely in the constant volume of a sealed vessel.
The triple point of water is the SI standard for temperature. Its assigned value is 273.16 oK (Kelvin). Originally, two fixed points were used to define standard temperature interval. They were the steam (the boiling point of water at standard atmospheric pressuresure) and the ice point (the melting point of ice when equilibrium with water saturated with air at standard atmospheric pressure).
The Celsius scale (or the centigrade scale), devised by the Swedish Anders Celsius (1701-1744), assigned the value O oC to the ice point and 100 oC to the steam point. Thus the interval between the two fixed points is 100 Co.
Kelvin temperatures have the unit oK. The magnitude of the Kelvin degree (Ko) is the same of that of the Celsius degree. These are arbitrarily established units for the measurement of temperature. Hence. O oK is called absolute zero.
Zero should not be thought of as a condition of matter with zero energy and no molecular motion. Molecular does not cease at absolute zero. The molecules of a substance at absolute zero have a minimum amount of kinetic energy, known as the zero-point energy. Molecular energy is a minimum, but not zero, at absolute zero.
Here is the equation to convert Celcius and Kelvin:
oK = oC + 273o
Note that on the Absolute Scale (Kelvin) there will be no negative numbers.
The most commonly used thermometers contain either mercury or alcohol. In both cases, the liquid volume increases rather uniformly with temperature over the useful range of the instruments.
8.3 Heat Units There is no instrument that directly measures the amount of thermal energy a body gives off or absorbs. Therefore, quantities of heat must be measured by the effects they produce. For example, the amount of heat given off when a fuel burns can be measured by measuring the temperature change in a known quantity of water that the burning produces. If one sample of coal warms 1.0 kg of water 1.0 Co, and another sample warms 1.0 kg of water 2.0 Co, then the second sample gives off twice as much heat.
In the past, water was the standard substance for defining heat units. In the metric system of units, the kilocalorie (kcal) was defined as the quantity of heat needed to raise the temperature of one kilogram of water one Celsius degree.
The calorie is defined as the quantity of heat needed to raise the temperature of one gram of water one Celsius degree.
Observe that a unit mass of water was used for defining each heat unit. Also note that the kilocalorie is one thousand times larger than the calorie. The kilocalorie is the "Calorie" used by biologists and dietitians to measure the fuel value of foods. Note that food "calories" are really kilocalories. That cookie really contains 1000 times the energy that it's rated! Romiso.
The foregoing definition of the calorie is still used in many laboratory measurements. However, as thermal measurements increased in precision, these older definitions became inadequate. Another reason is that the quantity of heat required to raise the temperature of 1 gram of water through 1 Celsius degree varies slightly for different water temperatures.
The calorie is also defined as a specific number of joules.
1 calorie = 4.1868 joules
Defined in this way, the size of the calorie is nearly the same as the original calorie. When taken to three significant figures, 4.19 joules, this slight difference disappears. Thus the relationships stated in the original definition are still useful in measuring thermal properties.
The kilocalorie and the kilogram are consistent with the SI units of measurement we have stressed throughout this book. They are often inconveniently large for laboratory and discussion purposes, however. We shall use calorie and gram units in our consideration of the thermal properties of matter because of their more practical size.
THERMAL EXPANSION
8.4 Thermal Expansion of Solids With few exceptions, solids expand when heated and contract when cooled. They not only increase or decrease in length but also in width and thickness. When a solid is heated, the increase in thermal energy increases the average distance between the atoms and molecules of the solid, and it expands.
The expansion of solids can be measured experimentally. A metal rod is heated in an apparatus that has a precise measuring device. If the temperature of an aluminum rod 1.0 m long is raised 1.0 Co, the increase in length is 2.3 x 10-5 m. An iron rod of the same length expands only 1.1 x 10-5 m when its temperature is raised 1.0 Co. For the same increase in temperature, different materials of the same length expand by different amounts.
The increase in length per unit length of a solid when its temperature is raised one degree is called its coefficient of linear expansion.
As mentioned, 1.0 m of aluminum expands 2.3 x 10-5 m when its temperature is raised 1.0 Co. The coefficient of linear expansion of aluminum is therefore 2.3 x 10-5/Co.
Likewise the coefficient of linear expansion of iron is 1.1 x 10-5/Co. Since the coefficient of linear expansion is defined as the change in length per unit length, its value does not depend upon any particular length unit. Appendix B, Table 14 gives the value of the coefficient of linear expansion of several solids.
Here is the equation for linear expansion:
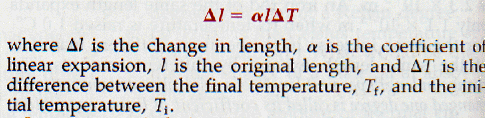
8.6 Abnormal Expansion of Water Suppose an expansion bulb is filled with pure water at OoC. As the bulb and water are warmed, the water gradually contracts until a temperature of 4oC is reached. As the temperature of the water is raised above 4oC, the water expands. Because the volume of water decreases as the temperature is raised from OoC to 4oC, the mass density of the water increases. (The mass of the water is constant.)
Above 4oC the volume of water increases as the temperature is raised, and the mass density decreases. Therefore, water has its maximum mass density, 1.0000 g/cm3, at 4oC. Never Forget this!
This unusual variation of the density of water with the temperature can be explained as follows. When ice melts to water at OoC, the water still contains groups of molecules bonded in the open crystal structure of ice.
As the temperature of water is raised from OoC to 4oC, these open crystal fragments begin to collapse and the molecules move closer together. The molecular speeds of the molecules also increase during the OoC to 4oC interval, but the effect of the collapsing crystal structure predominates and the density increases. Above 4oC the effect of increasing molecular speed exceeds the effect of collapsing crystal structure and the volume increases.
If water did not expand slightly as it is cooled below 4oC and expand much more as it freezes, the ice that forms on the surface of a lake would sink to the bottom. During the cold winter months, ice would continue to form until the lake was frozen solid. In the summer months only a few meters of ice at the top of the lake would melt.
However, because of the unusual properties of ice and water, no ice forms at the surface of a pond until all the water in it is cooled to 4oC. As the surface water cools below 4oC, it expands slightly and floats on the 4oC water. Upon freezing at OoC, further expansion takes place and the ice floats on the OoC water.
8.7 Charles' Law Gases expand when heated because the increase in the thermal energy of the gas molecules results in an increase in their kinetic energy. Different solids and liquids have different coefficients of expansion, but all gases have approximately the same coefficient of expansion.
Also, the coefficient of expansion of gases is nearly constant at all temperatures, except for those near the liquefying temperature of the gas. This was demonstrated experimentally in 1787 by French scientist Jacques Charles (1746-1823) in a manner similar to that described below.
Gas molecules are separated by distances much greater than their molecular diameters. Consequently, the forces acting between them, and their in relation to the total gas volume, are negligible. For these reasons all gases have similar physical properties at temperatures and pressures near those at which they liquefy.
Charles' law, can be stated thus: The volume of a dry gas is directly proportional to its Kelvin temperature, provided the pressure remains constant.
8.8 Boyle's Law The English scientist Robert Boyle (1627-1691) was the first person to investigate what he called the "spring elasticity of the air." Other scientists at that time knew about compressed air but none of them had performed experiments to learn how the volume of a gas is affected by the pressure exerted on it.
In his experiments, Boyle used a large J-shaped glass tube. He set up the apparatus in the stairwell of his laboratory at Oxford. The straight portion of the shorter arm was about one-third meter in length, while the longer arm had a length of about twenty-five meters.
Enough mercury was poured into the tube to fill the bent portion. By tipping the tube to allow air to escape from the small arm, the mercury levels were then adjusted so that the mercury would stand at the same height in both arms. In this way Boyle trapped a column of air in the short arm of the tube.
Next he measured the height of this air column. By assuming that the bore of the tube was uniform, Boyle used the height of the air column as a measure of the volume of air. The air in the short arm was at atmospheric pressure because the mercury levels were the same in both arms of the tube. See Figure 8-11(A).
In successive steps Boyle added more mercury to the long arm of the tube. By measuring the new height of the column of air in the short arm, he could determine each new volume. He found the corresponding pressure on this volume of air by measuring the height of the mercury column and adding that height to the atmospheric pressure as measured by a mercury barometer.
Boyle cooled the trapped, compressed air with a wet cloth, warmed it with a candle flame, and noted the resulting small changes in volume. These changes were so slight, however, that while it was obvious to Boyle that the temperature of the air during the experiment should be kept constant, small changes in temperature would not seriously affect the experimental results.
Boyle's data, though not exceedingly accurate, convinced him and other scientists of his time that "the pressures and expansions ... [are] in reciprocal proportion," Increasing the pressure on a column of confined air reduces its volume correspondingly. To reduce the volume to one-half, it is necessary to double the pressure; to reduce the volume to one-third, it is necessary to triple the pressure. Today we state
Boyle's law as follows: The volume of a dry gas varies inversely with the pressure exerted on it, provided the temperature remains constant.
When two quantities are in inverse proportion, their product is a constant. At any given temperature, the product of pressure and volume is always a constant.
pV = k
8.9 The Combined Gas Equation
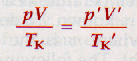
Where p is first pressure, V is first volume, Tk is first temperature (in K), and p' is new pressure, V' is new volume, and Tk' is the new temp (in K).
HEAT EXCHANGE:
8.11 Heat Capacity Blocks of five different m aluminum, iron, copper, zinc, and lead are shown in Figure 8-13. They all have the same mass and the cross-sectional area, but the pieces have different heights because the metals have different densities. First the blocks are put in a pan of boiling water to heat them all the same temperature. Then they are transferred to a block of paraffin. The diagram shows the relative depths which the metals melt the paraffin. The aluminum melts the most paraffin, iron follows as a poor second, copper and zinc are tied for third, and lead melts the least paraffin.

This demonstration shows that different materials absorb or give off different amounts of heat, even though the materials have the same mass and undergo the same temperature change.
Similarly, different amounts of heat are absorbed by blocks of the same material if their mass is different and their temperature change the same, if their mass is the same and their temperature change is different, or if they have different masses and undergo different temperature changes.
Such objects are then said to differ in heat capacity. Those with a high heat capacity warm more slowly because they absorb a greater quantity of heat; they also cool more slowly because they give off more heat. The heat capacity of a body is the quantity of heat needed to raise its temperature 1o.
8.22 Specific Heat The heat capacity of an object does not describe the thermal properties of the material of which it is made. For example, the heat capacity of 1.0 kg of copper differs from that of 1.0 kg of aluminum, but the heat capacity of 1.0 kg of aluminum also differs from that of 2.0 kg of aluminum. In order to obtain a quantity that is characteristic of copper, aluminum, or any material, the heat capacities of equal masses of the materials must be compared. This comparison yields a more useful quantity known as specific heat.
Specific heat is the heat capacity of a material per unit mass. It is numerically equal to the quantity of heat that must be supplied to a unit mass of a material to raise its temperature one degree. Here is the formula to determine the quantity of heat:
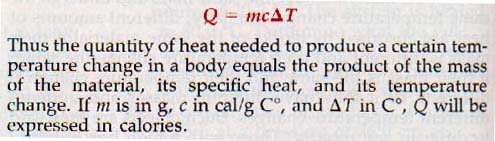
8.13 Law of Heat Exchange Hot water can be cooled by the addition of cold water. As the two mix, the temperature of the hot water is lowered while the temperature of the added cold water is raised.
The final temperature of the mixture lies between the original temperatures of the hot and cold water. Each time two substances of unequal temperature are mixed, the warmer one loses heat and the cooler one gains heat until both finally reach the same temperature.
A process that absorbs heat as it progresses is endothermic. An exothermic process gives off heat as it progresses.
No thermal energy is lost when substances of unequal temperatures are mixed. In any heat-transfer system, the heat lost by hot substances equals the hear gained by cold substances. This is known as the law of heat exchange. The total number of heat units liberated by warmer substances equals the total number of heat units absorbed by cooler substances. This can be expressed as
Heat Lost = Heat gained
Qlost = Qgained
This equality is the basis of a simple technique known as the method of mixtures for measuring a quantity of heat in transit from one substance to another. The method of mixtures and the law of heat exchange can be used to determine the specific heat of a solid.
The hot solid of unknown specific heat, but of known mass and temperature, is "mixed" with water of known mass and temperature in a calorimeter (usually nested metal cups separated by an insulating air space) of known mass and temperature.
The final temperature of the mixture is measured. All the data for the law of heat exchange equation are known except the specific heat of the solid. It can be calculated as in the examples. In practical situations, some heat is usually transferred to the surroundings. This decrease in the amount of thermal energy that can be measured affects the accuracy of most heat experiments in the high school laboratory.
CHANGE OF PHASE
8.14 The Triple Point The phase and density of pure substance are determined by its temperature and pressure. When temperature and pressure are controlled it is possible to cause a pure substance to change from one phase to either of the other two phases. The substance can make the phase change directly or by first through the third phase.
Figure 8-15
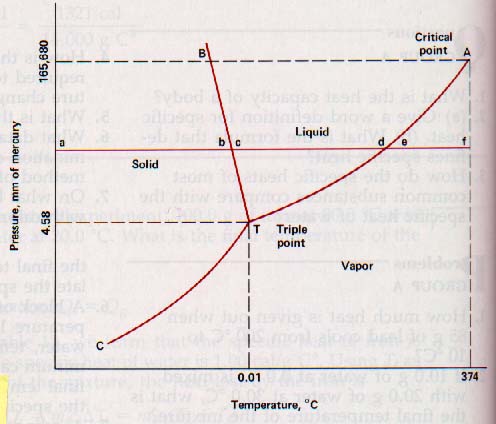
Figure 8-15 is the temperature-pressure graph for water. At the pressure and temperature of triple point, T, the three phases of water can exist in equilibrium. It exists as a solid for temperature-pressure values lying in the area between the curves TC and TB. It is liquid when these values lie in the area between TB and TA.
In the area below the ATC curve it is a vapor. If the temperature-pressure values fall anywhere on the curve TA, water can exist with its vapor and liquid phases in equilibrium.
Similarly, if these values fall on the curve TB the solid and liquid phases can exist in equilibrium. For values on the curve TC the solid and vapor phases exist in equilibrium.
When there are two or more phases of a substance in equilibrium at any given temperature and pressure, there will always be interfaces separating the phases.
Figure 8-15 (with the solid-liquid curve TB, the liquid-vapor curve TA, and the solid-vapor curve TC plotted on a single graph) is typical of pure crystalline materials. However, each substance has a different set of curves. This is because the temperatures at which changes of phase occur (at a given pressure) are different for each substance.
Other features of the graph in Figure 8-15 will be explained in succeeding sections of this chapter. So it is important that you fully understand the meaning of the lines TA, TB, and TC in the figure.
8.15 Heat of Fusion At the temperature and pressure indicated by point a in Figure 8-15, water exists as ice, a solid. Let us assume that we keep the pressure constant as we apply heat at a uniform rate. The ice will be warmed from its initial temperature to the temperature at point b. At this temperature the ice will begin to melt. Melting is an endothermic process. The application of more heat will melt more ice, but the temperature will not rise until all the ice is melted.
Following this change in phase, the temperature of the liquid water will rise. The horizontal line abcdef shows the temperature values as heat is applied first to the ice, then to the water, and finally to the vapor while the pressure on the system is held constant.
This information can be shown more strikingly in another way. Assume that we start with a block of ice at -20oC and add heat at a constant rate while holding the pressure constant at a value indicated by the line af. A plot of temperature readings against time during which heat is being applied at a uniform rate gives us the graph in Figure 8-16. The line ab in each figure represents the warming of the ice without change of state; bc represents the heat required to change the solid to a liquid without a change of temperature (note that b and c of Figure 8-16 are the same point); cd represents the warming of the water.
The addition of heat to a solid at its melting point produces a change of phase instead of a rise in temperature. All the heat energy is used to increase the potential energy of the particles. The average kinetic energy is unchanged. Thus the addition of heat to ice at a pressure of one atmosphere and a temperature of OoC causes the ice to change into water at OoC.
The amount of heat needed to melt a unit mass of a substance at its melting point is called its heat of fusion, Lf. Lf for ice is approximately 80 cal/g at OoC, meaning that this quantity of heat must be added to each gram of ice at OoC to convert it to water at OoC. Heats of fusion of various substances are given in Appendix B, Table 13
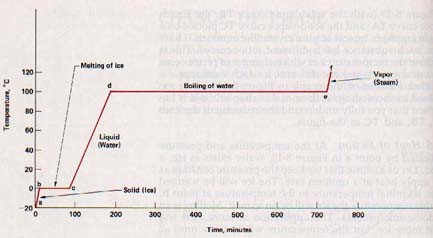
8.16 The Freezing Process The heat added to ice to make it melt increases the thermal energy of its molecules and changes it into water. This same amount of heat is evolved when water freezes because this process is a reversible energy change. Freezing is an exothermic process. Each gram of water at OoC that forms ice at OoC liberates approximately 80 calories of heat. When the molecules of water return to their fixed positions in ice, they give up in the form of heat the energy that enabled them to slide over one another.
The reversible energy change between 1 g of ice and 1 g of water at OoC depends upon whether head is added or subrtacted. To change the ice to water, it is necessary to add 80 cal; to change the water to ice, it is necessary to take away 80 cal.
If pure water is very carefully cooled without being disturbed, it can reach temperatures as low as -20oC without freezing. Water that is cooled below the normal freezing point is said to be supercooled.
If a piece of ice or a speck of dust is added to such water, freezing takes place rapidly and the temperature rises to OoC, the normal freezing point. The formation of ice takes place readily at OoC if there is some dust or other foreign matter on which the first crystals of ice can form.
Supercooling occurs when no such foreign matter is present. Supercooling is of particular interest in meteorology because the process of supercooling takes place in the formation of some clouds and when "freezing rain" turns to ice as it hits trees, telephone wires, and other surfaces.
8.17 The Boiling Process The equilibrium vapor pressure of a liquid is a characteristic of the liquid that depends on the temperature only. Appendix B, Table 12, gives the equilibrium vapor pressure of water at various temperatures.
The vapor pressure curve for water is shown in Figure 8-18.
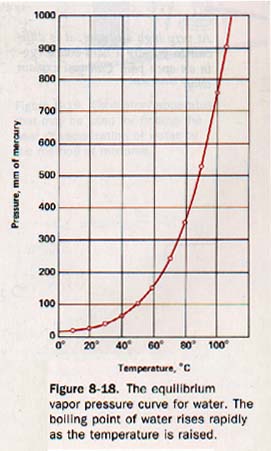
This curve shows the relationship between the pressure and temperature of water and its saturated vapor. Any point on the curve represents a definite temperature and pressure at which water is in equilibrium with its saturated vapor.
Other liquids show vapor pressure curves that are similar. Solids, like liquids, exert a vapor pressure. The equilibrium vapor pressure of ice at OoC is about 4.5 mm of mercury. The vapor pressure of solids is much less than that of liquids because solids sublime more slowly, if at all, at normal temperatures.
Evaporation of both solids and liquids can occur at temperatures and pressures other than the equilibrium values that fall on the curves TC and TA of Figure 8-15. A solid at any temperature and pressure to the left of the curve TC can be evaporating to some degree depending upon the nature of the substance. Under these conditions the vapor pressure of the substance will be less than the pressure at saturation, however.
At 100oC the vapor pressure of water is 760 mm of mercury. 100oC is the normal boiling point of water.
If the air pressure is reduced to 525 mm of mercury, water boils at 90oC because at this temperature the vapor pressure of water is 526mm of mercury.
In order to make water boil at 50oC, the pressure must be reduced to 92.5 mm of mercury. If the pressure is increased to 787 mm of mercury, water will not boil until l01oC .
Strong-walled pressure cookers, in which water is boiled at pressures up to about 2 atmospheres and at temperatures up to about 120oC, are useful for rapid cooking of foods. Special pans in which water is boiled at room temperature or slightly above are used in the production of sugar crystals.
If a mixture of ethanol and water is boiled the boiling temperature is not the same as the boiling point of either liquid by itself. Ethanol boils at 78oC and water at 100oC. The boiling temperature of the mixture is between 78oC and 100oC , depending on the proportions of ethanol and water in the mixture.
The boiling temperature of a mixture of two or more liquids each having different boiling points is different from that of any of the liquids used. A liquid can be separated from a nonvaporizing dissolved solid by distillation.
Distillation involves evaporation followed by condensation of the vapor in a separate vessel. Liquids that have different boiling points can be separated by fractional distillation. As the mixture boils, more of the component with the lower boiling point vaporizes and the boiling point of the resulting mixture rises. Samples collected at different temperatures are then redistilled.
8.18 Heat of Vaporization heated to 100oC, each gram of water will absorb 10~~ cal. If
If a liter of water at OoC is heated to 100oC, each gram of water will absorb 100 cal. If heat is supplied at a constant rate it takes more than five times as long to boil the water away as it did to heat it from OoC to 100oC. (See Figure 8-16.)
Each gram of water absorbs more than 500 calories of heat as it is changed into steam. The temperature of the water remains constant during boiling, and the steam produced has this same temperature as the boiling water. The heat required per unit mass to vaporize a liquid at its boiling point is called its heat of vaporization, Lv
The heat required for vaporization gives the particles of liquid sufficient thermal energy to overcome the energy binding them to the liquid, and so enables them to separate from one another and move among the molecules of the gases above the liquid.
As noted in Section 7.20, all the energy is used to increase the potential energy of the particles. Their average kinetic energy is not changed. Since the energy required for vaporization varies with temperature, the heat of vaporization varies with temperature.
The heat of vaporization for water is about 539 cal/g at 100oC. Water boiling under reduced pressure at a lower temperature has a heat of vaporization that is somewhat greater; at boiling temperatures above the normal boiling point, the heat of vaporization is smaller.
The method of mixtures is used to determine the heat of vaporization of water. As shown in Figure 8-19, a known mass of steam is passed into a known mass of cold water at a known temperature, and the increase in temperature is measured.
8.19 The Condensing Process Heat is absorbed during vaporization. This increase in the thermal energy of the molecules of a liquid enables them to break away from liquid and become molecules of vapor.
When the vapor condenses to a liquid, this thermal energy is evolved as heat. This reversible energy change is useful in a steam-heating system.
The heat of vaporization changes water to steam in a boiler. The steam passes into radiators where it gives its heat of vaporization and condenses to a liquid. Even though steam and boiling water are at the temperature, steam can produce a more severe burn. One reason is that steam at 100oC has acquired about 540 calories of heat per gram than water at 100oC. When steam condenses, this heat of vaporization is given out. As it cools, the water that is formed gives out the same amount of heat that water at 100oC does during cooling.
In order to keep the pressure constant while heat is applied to change ice from -20oC to steam at 120oC, the volume of the container must be greatly increased.
In our previous discussions we noted that ice expands slightly as its temperature is raised to 0oC, it contracts as it is melted to water at 0oC, the water formed contracts to its minimum volume at 4oC, and above 4oC the water expands as its temperature is raised to 100oC.
At constant pressure, as the water at 100oC is changed to steam at 100oC by the addition of heat the expansion is about 1700 times. As the vapor (steam) is heated further, it continues to expand.
8.20 The Critical Point The vaporization curve TA in Figure 8-15 is not unlimited in extent. The lower limit is the temperature and pressure of the triple point. The upper limit is the critical point.
The temperature and pressure of the critical point are called the critical temperature and the critical pressure.
A substance cannot exist as a liquid at a temperature above its critical temperature; no matter how great the pressure, it cannot be condensed to the liquid state.
At the critical point the densities of the liquid and the vapor are equal and the heat of vaporization is zero. At temperatures above the critical temperature a substance is usually called a gas, while at temperatures below the critical temperature it is called a vapor.
The critical temperature of water is 374 oC, and the critical pressure is 218 atmospheres. This means that the temperature of liquid water cannot be raised to 374oC unless it is under a pressure of 218 atmospheres, and that at any higher temperature water can exist only in its gaseous phase, no matter how high the pressure.
Gaseous substances, such as oxygen and nitrogen, have very low critical temperatures. The critical temperature of oxygen is -119oC and of nitrogen is -174oC. These gases must first be cooled to their low critical temperatures before they can be liquefied. Helium has the lowest critical temperature, -268oC.
SUMMARY
The thermal energy of a material is the potential and kinetic energy of its particles. Heat is the thermal energy that is absorbed, given up, or transferred from one material to another. Thus heat is a form of energy.
Temperature is the physical quantity that is proportional to the average kinetic energy of the particles of a substance.
Temperature is measured in degrees. The Celsius and Kelvin temperature scales are based on the triple point of water, which is the temperature at which the solid, liquid, and vapor phases of water can coexist. Absolute zero (OoK) is the temperature at which the kinetic energy of the molecules of a substance is at a minimum.
Heat is measured in calories. A calorie is equivalent to 4.19 joules of energy.
The change in unit length of a solid when its temperature is changed one degree is its coefficient of linear expansion. The expansion of most liquids is proportional to their increase in temperature. The expansion of water is abnormal. Water reaches its maximum density at 4 oC.
Gases expand uniformly except at very high pressures and very low temperatures. According to Charles' law, the volume of a dry gas is directly proportional to its Kelvin temperature provided the pressure is constant.
Boyle's law states that if the temperature is constant, the volume of a dry gas is inversely proportional to the pressure. The universal gas constant relates the pressure, volume, Kelvin temperature, and number of moles of an ideal gas.
The heat capacity of a body is the quantity of heat needed to raise its temperature one degree. Its specific heat is the ratio of its heat capacity to its mass.
The heat given off by hot materials equals the heat received by cold materials.
The heat of fusion is the amount of heat needed to bring about fusion in a unit mass of a substance at its melting point.
The heat required to vaporize a unit mass of liquid at its boiling point is the heat of vaporization.
The temperature to which any gas must be cooled before it can be liquefied by pressure is called its critical temperature; the pressure needed to liquefy a gas at this temperature is called its critical pressure.
VOCABULARY
Boyle's law, calorie, calorimeter, Celsius scale, Charles' law, coefficient of linear, expansion, critical point, critical pressure, critical temperature, endothermic, exothermic, heat, heat capacity, heat of fusion, heat of vaporization, Kelvin scale, law of heat exchange, mole, specific heat, standard pressure, standard temperature, temperature, thermal energy, triple point.
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester