CONSERVATION OF ENERGY & MOMENTUM

WORK, MACHINES, AND POWER
CONSERVATION OF ENERGY & MOMENTUM

WORK, MACHINES, AND POWER
6.1 Definition of Work The word work has a specific meaning in physics. Work is done when a force is exerted on an object causing the object to move in the direction of a component of the applied force. Even if you hold a heavy load on your shoulder, as long as you do not move you are not doing any work on the load. You are merely exerting an upward force that counteracts the downward force of gravity on the load.
You do work in a scientific sense when you raise the load to your shoulder, when you carry it up a flight of stairs, or when you pull it across the floor. In these cases, you exert a force that has a component in the direction in which the object moves.
Two factors must be considered in measuring work: the displacement of the object and the magnitude of the force in the direction of displacement. The amount of work, W, equals the product of the force, F, in the direction of displacement and the displacement, d, of an object.
W = Fd
When the force is measured in newtons and the distance through which it acts is measured in meters, the work is expressed in joules (j).
A force of one newton acting through a distance of one meter does one joule of work. This unit of work is named for the English physicist James Prescott Joule. Note that a joule is a newton meter.
For example, let us compute the work required to lift a l.O-kg mass to a height of 5.0 m. From the relationship between mass and weight discussed in previous chapters, we know that a force of about 9.8 n must be exerted to lift a mass of 1.0 kg at sea level. Thus, the amount of work involved is
W = Fd
W = (9.8 n)(5.0 m)
W = 49 j
If we merely slide the l.O-kg mass at constant velocity along a horizontal surface having a coefficient of sliding friction of 0.30 for a distance of 5.0 m, the work required is
W = Ff d
W = (0.30)(9.8 n)(5.0 m)
W= 15 j
In both instances, the force is applied in the direction in which the object moves.
Suppose, however, that the force is applied to the object in a direction other than that in which it moves. In that case, only the component of the applied force that acts in the direction the object moves is used to compute the work done on the object. Ah vectors!
6.2 Work Done by Varying Forces In the examples of work in Section 6.1, the forces involved did not vary. In many problems involving work, however, the forces may vary in direction, in magnitude, or in both during the time that they are acting on an object. For example, when a force is used to stretch a spring, the magnitude of the force increases as the spring gets longer.
An easy way to determine the amount of work done by a varying force is to use a graph. The area under the curved line represents the work done by a force that varies in magnitude.
To calculate the area of a geometric figure that is bounded by one or more curved lines requlres a branch of mathematics called the calculus. A good approximation is obtained, however, by the use of suitable rectangles. The total amount of work that is represented by the area under the curve can be found by adding the areas of many rectangles formed.
The problem of finding the total work done by a varying force is somewhat simpler in the case of a stretching spring, as long as the force is constantly applied in the direction of the stretching.
The force required to stretch a spring depends on the stiffness of the spring, but the force is directly proportional to the amount of stretching.
6.3 Work in Rotary Motion To compute the work done in rotary motion, we use this formula:

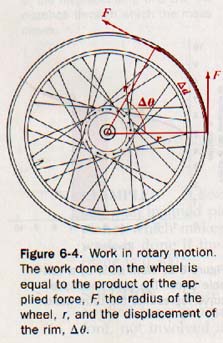
MACHINES
6.4 Machines Six types of simple machines are shown in Figure 6-5. Each one can be used to multiply force. Other machines are either modifications of these simple machines or combinations of two or more of them. The six machines shown are actually variations of two basic types: the pulley and the wheel and axle are forms of the lever, and the wedge and screw are modified inclined planes.
Although a machine can be used to multiply force, it cannot multiply work. The work output of a machine cannot exceed the work input. In a frictionless machine, work output and work input would be exactly equal. In a machine that multiplies force, this equality means that the distance over which the input force moves is always greater than the distance over which the load moves.
The ratio of the useful work output of a machine to total work input is called the efficiency.
Efficiency = Woutput / Winput
The efficiency of all machines is less than 100% because the work output is always less than the work input. This is due to the force of friction.
Thus in using a machine to lift an object, the efficiency equation becomes
Efficiency = Fwh / Fad
Figure 6-5.
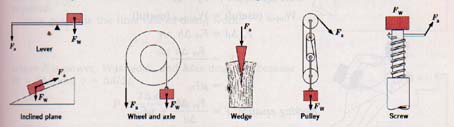
Simple machines. Each machine multiplies force at the expense of distance.
6.5 Definition of Power Like the term work, the term power has a scientific meaning that differs somewhat from its everyday meaning. When we say a person has great power, we usually mean that the person has great strength or wields great authority. In physics, the term power means the time rate of doing work.
You do the same amount of work whether you climb a flight of stairs in one minute or in five minutes, but your power output is not the same. See Figure 6-7. Power depends upon three factors: the displacement of the object, the force in the direction of the displacement, and the time required.
Since power is the time rate of doing work,
P = W /t
where P is power, W is work, and t is time. Or, because W = Fd and v = d /t,
P = Fd /t
P = Fv
When work is measured in joules and time is measured in seconds, power is expressed in watts (w). A watt is a joule per second. This unit is named in honor of James Watt who designed the first practical steam engine. Since the watt is a very small unit, power is more commonly measured in units of 1000 watts, or kilowatts (kw).
6.6 Power in Rotary Motion

ENERGY
6.7 Gravitational Potential Energy In Chapter 1 we saw that there are two kinds of energy, potential and kinetic. In the following sections, we will deal quantitatively with these concepts and see how the various forms of energy are expressed in terms of work units.
The potential energy acquired by an object equals the work done against gravity or other forces to place it in position. The equation for calculating work when the force acts in the same direction as the displacement is W = Fd
Therefore the equation for potential energy is
Ep = Fd
In lifting an object, F is its weight, which from Newton's second law of motion equals mg, and d is the vertical distance h through which it is lifted. Hence the potential energy equation can be written
Ep = mgh
The gravitational potential energy defined by this equation is expressed in relation to an arbitrary reference level where h = O. It makes no difference what level is chosen. Sea level, street level, ground level, or floor level are all useful reference levels.
When the mass of an object is given in kilograms, the height in meters, and the acceleration due to gravity in m/s2, the gravitational potential energy is expressed in joules. Thus if a 50 kg mass of steel is raised 5.0 m, its gravitational potential energy is
EP = mgh
Ep = 50 kg X 9.8 m/s2 X 5.0 m
Ep = 2.5 X 103 j
6.8 Kinetic Energy in Linear Motion As we saw in Section 3.7, the velocity of a freely falling object that starts from rest, expressed in terms of the acceleration of gravity and the distance traveled, is given by the equation
v = square root of (2gd)
by substitution we get
Ek = mv2/2
Although this equation for kinetic energy was derived the motion of a falling body, it applies to motion in direction or from any cause.
As in the case of gravitational potential energy, kinetic energy is expressed in joules if the mass is given in kilograms and the velocity in meters per second. Thus if a baseball has a mass of 0.14 kg and is thrown with a velocity of 7.5 m/s, its kinetic energy is
Ek = 0.14 kg (7.5 m/s)2 / 2
Ek = 3.9 j
6.9 Kinetic Energy in Rotary Motion

6.10 Elastic Potential Energy When a spring is compressed, energy is stored in the spring. At any instant during the compression, the elastic potential energy in the spring is equal to the work done on the spring. The potential energy in a stretched or compressed elastic object is called elastic potential energy.
The work required to stretch or compress a spring does not depend on the weight of the spring. Consequently, gravity is not involved in the measurement of elastic potential energy. Instead, the work required to stretch or compress a spring is dependent upon a property of the spring known as the force constant. The force constant does not change for a specific spring so long as the spring is not permanently distorted.
The force required to stretch a Spring is written as
F = kd
where k is the force constant of the spring and d is the distance over which F is applied. We noted in Section 6.2 that the force is directly proportional to the amount of stretching (within definite limits). Consequently, the work done on the spring also varies directly with the amount stretching. The total amount of work, therefore, is by the equation
W = Fd / 2
where F is the force exerted on the spring at the end of stretch through distance d. Because the force varies zero to F, the equation uses the average of these two values or F / 2
Substituting get
Ep = kd2 / 2
where Ep is the elastic potential energy. This equation resents ideal conditions. In actual practice, a small fraction of the work of stretching or compression is converted into heat energy in the spring and thus does not show up elastic potential energy.
6.21 Conservation of Mechanical Energy As we in Section 5.10, the vibration of a mass on a spring and swinging of a pendulum are both examples of simple harmonic motion. Both can also be used to illustrate an important principle of physics called the law of conservation of mechanical energy.
This law states that the sum of the potential and kinetic energy of an energy system remains constant when no dissipative forces act on the system. Gravitational forces and elastic forces are called conservative forces because they conform to the law of conservation of mechanical energy.
There are forces, however, that produce deviations from the law of conservation of mechanical energy. The force of friction is an example. Forces of this type are called nonconservative, or dissipative forces. The reason that friction is a dissipative force is that it produces a form of energy (heat) that is not mechanical. Energy is lost to the system.
When considered in light of the more comprehensive law of conservation of total energy, there is no "lost" energy, of course. The calculation of heat energy and its role in energy transformations will be discussed in Chapter 8.
Another way to distinguish between conservative and dissipative forces is to observe the relationship between the force and the path over which it acts. In the case of a conservative force, the work done and energy involved are completely independent of the length of the path, provided the paths have the same end point.
For example, in the illustration of gravitational potential energy in Figure 6-13,
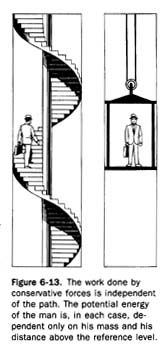
the gravitational potential energy of both men is the same, provided they have equal masses, even though one of them traveled a greater distance than the other one. The mass of the men and their height above the reference level are the only factors necessary for the determination of gravitational potential energy.
The amount of heat energy lost through friction, a dissipative force, can be quite different for two objects moving through the same height, however. Where the path is longer, the amount of mechanical energy that is converted to heat energy will be greater. This is true even if the frictional forces were to remain constant. Thus the work done by a given dissipative force varies directly with the length of the object path.
MOMENTUM
6.2 The Nature of Momentum More force is needed to stop a train than to stop a car, even though both are moving with the same velocity.
A bullet fired from a gun has more penetrating power than a bullet thrown by hand, even though both bullets have the same mass. The physical quantity that describes this aspect of the motion of an object is called momentum. Momentum is the product of the mass of a moving body and its velocity. The equation for momentum is
p = mv
where p is the momentum, m is the mass, and v is the velocity of an object.
In the example of the car and train, the greater mass of the train gives it more momentum than the car. Consequently, a greater change of momentum is involved in stopping the train than in stopping the car. In the case of the bullets, the greater momentum of the fired bullet is due to its greater velocity; a large change of momentum takes place when the speeding bullet is stopped. From Newton's second law of motion, we can derive an important relationship involving momentum. We know that over a short time interval
aav = v / t (Section 3.5).
If we substitute this value of acceleration for a in F = ma, we get
F = mv/t
or
Ft = mv
The product of a force and the time interval during which it acts, Ft, is called impulse. Hence from Newton's second law of motion we have established that impulse equals change in momentum.
The equation F = mv/t tells us that when a force is applied to a body, the body's rate of change of momentum is equal to the force.
Since the equation is a vector equation, we also know that the body's rate of change of momentum is in the direction of the force. A good example of the relationship between impulse and change in momentum is a bat hitting a baseball.
The impulse imparted to the ball depends on the force with which the ball is hit and the length of time during which the ball and bat are in contact. On leaving the bat, the ball has acquired a momentum equal to the product of its mass and its change of velocity. In a sense, the impulse produced the change of momentum; hence the two are equal.
6.13 The Conservation of Momentum In Figure 6-15, a boy with a mass of 40 kg and a man with a mass of 80 kg are standing on a frictionless surface. When the man pushes on the boy from the back, the boy moves forward and the man moves backward.
The velocities with which the boy and the man move are specified by one of the most important principles of physics, the law of conservation of momentum. This law states that when no net external forces are acting on a system of objects, the total vector momentum of the system remains constant.
Let us apply this law to the situation in Figure 6-15. Initially the man and the boy are at rest. The system, therefore, has zero momentum. When the man and the boy move apart, the law of conservation of momentum requires that the total vector momentum remain zero.
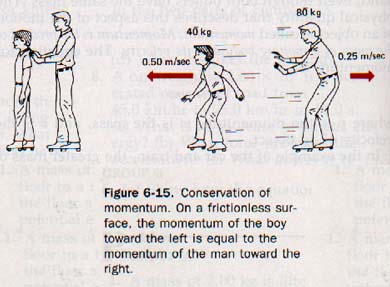
Hence the momentum of the boy in one direction must equal that of the man in the other direction. If the boy moves with a velocity of 0.50 m/s, the man will move with a velocity of 0.25 m/s since the mass of the man is twice as great as that of the boy. The momentum of the boy in one direction (40 kg x 0.50 m/s) must equal the momentum of the man in the opposite direction (80 kg x 0.25 m/s).
An important application of the law of conservation of momentum is the launching of a rocket. When a rocket fires, hot exhaust gases are expelled through the rocket nozzle. The gas particles have a momentum equal to the mass of the particles multiplied by their exhaust velocity. Momentum equal in magnitude is therefore imparted to the rocket in the opposite direction. Newton's third law of motion (Section 3.10) is a special case of the law of conservation of momentum.
6.14 Inelastic Collisions The law of conservation of momentum is very helpful in studying the motions of colliding objects. Collisions can take place in various ways, and we shall see how the momentum conservation principles apply in several such cases.
In Figure 6-17(A), two carts of equal mass approach each other with velocities of equal magnitude. A lump of putty is attached to the front of each cart so that the two carts will stick together after the impact. This situation is an example of inelastic collision.
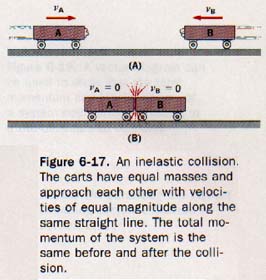
Since the carts are traveling along the same straight line, it is also an example of a collision in one dimension.
The momentum of cart A is mAvA. It is equal in magnitude to the momentum of cart B, mBvB. However, the direction of vA is opposite to the direction of vB, so
vA = -vB
Consequently,
mAvA = -mBv
and
mAvA + mBvB = O
This means that the total vector momentum of the system of two moving carts is zero. (We assume that the system is isolated, that is, there are no net external forces acting on it.
In actual collision studies, the external force of friction is usually minimized by using rolling carts or air tracks.
After the carts collide, they both come to rest. The cart velocities, vA and vB, are now both zero; the sum of the momenta of the two carts is zero, just as it was when the carts were in motion in opposite directions.
Thus the total vector momentum of the system is unchanged by the collision. If one of the carts has a greater mass than the other, although its velocity is still of equal magnitude but opposite sign, the outcome of the collision is different. After impact, the combined carts will move in the direction of the cart with the larger mass. The velocity of the combined carts will be such that the total momentum of the system remains unchanged. For example, suppose
mA = 2mB
and
vA = -vB, as before.
Then,
mAvA + mBvB are mot equal; to O
Since
mB + mA/2,
by substitution,
mAvA - mAVA/2 = mAVA/2
This means that the total momentum of the system, before and after the collision, is 1/2 mAvA; the combined carts will move with this momentum in the direction of the original velocity of cart A. The velocity after the collision can be found by dividing the total momentum by the total mass
When carts of equal and opposite momenta collide inelastically, they come to rest. Before the collision they have kinetic energy; after the collision, they do not. This is typical of all inelastic and partially elastic collisions.
Much or all of the kinetic energy that the moving objects have before collision is converted into heat or some other form of energy. If all these forms of energy are taken into account, the law of conservation of energy holds true for inelastic collisions. But kinetic energy alone is not conserved.
6.15 Elastic Collisions When colliding objects rebound from each other without a loss of kinetic energy, a perfectly elastic collision has just occurred. The only perfectly elastic collisions occur between atomic and subatomic particles.
The situation can be approximated, however, by the use of hard steel balls or springs on an air track. The momentum conservation law holds for elastic collisions as well as inelastic ones and for collisions that are partly elastic and partly inelastic.
The law also holds for collisions in two dimensions, that is, when the colliding objects meet at an angle other than head-on. Ball B collides at an angle with ball R, which is initially at rest. A vector diagram represents the momenta of the balls before and after collision.
So it follows from the laws of conservation of energy and momentum that, when a moving ball strikes a stationary ball of equal mass other than head-on in an elastic collision, the two balls move away from each other at right angles. The conservation of momentum also holds for collisions involving more than two bodies and in three-dimensional situations.
6.26 Angular Momentum For rotary motion, the relationship between impulse and the change of angular momentum is similar to that for linear motion. Using the symbols for rotary motion, the equation becomes
Tt = Iω f - Iω i
where Tt is the angular impulse and Iω f - Iω i is the change in angular momentum.
The dimensions of both angular impulse and angular momentum are kg m2/s. Just as the linear momentum of an object is unchanged unless a net external force acts on it, the angular momentum of an object is unchanged unless a net external torque acts on if. This is a statement of the law of conservation of angular momentum.
A rotating flywheel, which helps maintain a constant angular velocity of the crankshaft of an automobile engine, is an illustration, The rotational inertia of a fly-wheel is large.
Consequently torques acting on it do not produce rapid changes in its angular momentum. As the torque produced by the combustion in each cylinder tends to accelerate the crankshaft, the rotational inertia of the flywheel resists this action.
Similarly, as the torques produced in the cylinders where compression is occurring tend to decelerate the crankshaft, the rotational inertia of the flywheel resists this action and the flywheel tends to maintain a uniform rate of crankshaft rotation.
If the distribution of mass of a rotating object is changed, its angular velocity changes so that the angular momentum remains constant. A skater spinning on the ice with arms folded turns with relatively constant angular velocity. If she extends her arms, her rotational inertia increases. Since angular momentum is conserved, her angular velocity must decrease.
SUMMARY
Work is the product of a displacement and the component of the force in the direction of the displacement. The unit of work is the joule. Work done by varying forces can be found by calculating the area under the curve of a graph in which the horizontal axis denotes the displacement and the vertical axis denotes the force. Radian measure is used to compute work done in rotary motion.
Machines can be used to multiply force at the expense of distance. The efficiency of a machine is the ratio of the useful work output to the total work input and is expressed as a percentage.
Power is the time rate of doing work. It is measured in watts. Radian measure is used to compute power in rotary motion.
Gravitational potential energy is equal to the work done against gravity to place an object in position. Thus energy is measured in units of work. The kinetic energy of a body moving in a straight line is directly proportional to the mass of the body and the square of its velocity. In rotary motion, the kinetic energy is directly proportional to the rotational inertia and the square of the angular velocity.
Elastic potential energy is directly proportional to the force constant and the square of the amount of stretch. The law of conservation of mechanical energy states that the sum of the potential and kinetic energy of an ideal energy system remains constant.
Momentum is the product of the mass of a moving body and its velocity. The change of momentum of a moving body is equal to its impulse, which is the product of a force and the time interval during which the force acts.
The momentum of a system of objects is conserved when no net external forces are acting on the system. This is the law of conservation of momentum. The reaction principle is an application of this law. The conservation of momentum also helps to describe the motion of objects colliding elastically or inelastically and in one, two, or three dimensions. Unless a net external torque acts on a rotating object, its angular momentum is also conserved.
VOCABULARY
angular impulse, angular momentum, efficiency, elastic collision, elastic potential energy, gravitational potential energy, impulse, inelastic collision, joule, kinetic energy, law of conservation of mechanical energy, law of conservation of momentum, machine, momentum, power, watt, work
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester