TWO-DIMENSIONAL & PERIODIC MOTION

TWO-DIMENSIONAL & PERIODIC MOTION

Christian Huygens developed the equation for centripetal acceleration. He also invented a pendulum-controlled clock and originated the wave theory of light, which was in opposition to the particle theory of light proposed by Newton. The two famous scientists were contemporaries.
CIRCULAR MOTION
5.1 Motion in a Curved Path In Chapters 3 and 4, we studied the motion of objects along a straight line. Now let us examine what happens to the motion of an object that moves horizontally with uniform velocity but is also accelerated vertically. That is, there is a right angle between the direction of the uniform velocity (and the direction of the acceleration.
What will be the path of such an object? The ball in Figure 5-1 illustrates such motion. It was released at the same time as the ball on the left, but had a uniform horizontal velocity. The horizontal distances between adjacent images of the right-hand ball are equal. This indicates that the ball is still traveling horizontally with uniform velocity.

At the same time, the ball on the right covered the same vertical distance between each image as did the ball on the left, which had no horizontal velocity. Each position of the ball on the right is the resultant of motion with uniform velocity in one direction and with uniform acceleration in the other.
This two-dimensional combination produces motion along a curved path. Suppose a rifle bullet is fired horizontally with a velocity of 1250 m/s. Neglecting air resistance, the bullet travels 1250 m horizontally by the end of the first second.
Immediately after it leaves the muzzle of the gun, the force of gravity begins to accelerate the bullet toward the earth's center of gravity. This force is vertical. During the first second, a freely falling body drops 4.90 m. The bullet drops 4.9O m while traveling the first 1250 m horizontally. See Figure 5-2. In two seconds the bullet travels 2500 m horizontally, at which time it also drops vertically through a distance of 19.6 m.
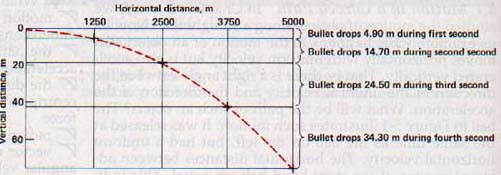
Over short distances the path of a high-velocity projectile approximates a straight line, but over greater distances its path is noticeably curved. If the line of sight to a target is horizontal, a projectile must be fired at a small upward angle in order to hit the target. This angle compensates for the downward acceleration due to the force of gravity on the projectile.
Provided the same ammunition is used, the size of this angle depends upon the distance to the target. The front sight of most rifles is fixed at the end of the barrel while the rear sight is movable. Since the line of sight is a straight line to the target, the angle the barrel makes with this line is increased by raising the rear sight.
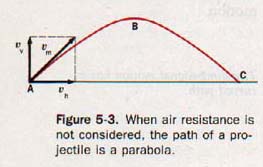
When the rifle is aimed, its muzzle is directed upward at the predetermined angle. When the gun is fired, this angle gives the bullet the upward velocity component necessary to compensate for the bullet's drop on its way to the distant target. The path a projectile takes if it is fired at an upward angle is shown in Figure 5-3. The path of the projectile, ABC, is called the trajectory.
5.2 Motion in a Circular Path An important type of two-dimensional motion is motion in a circular path, as seen in Figure 5-4. Ball A is attached to the end of string CA. The string is fastened at C. If the speed of the ball in the circular path is constant, the ball is said to describe uniform circular motion.
If the speed of the ball in the circular path varies, its motion is variable circular motion. Imagine that you are at a location where there is no force of gravity. You attach a ball to a string as shown in Figure 5-4 and hold the string at C. Then you give the ball an initial velocity in the direction of B, tangent to the circumference of the circle. The ball whirls in a circular path around C.
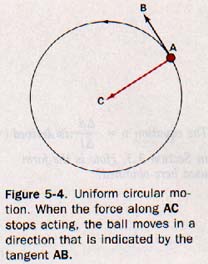
You can feel yourself pulling continuously on the string to keep the ball in the circular path. Let us analyze what you would observe in this situation. We know that the radius of a circle, AC for example, is perpendicular to the tangent drawn through the end of the radius.
If the string is in the direction of the radius and the velocity is always directed along a tangent, your pull on the string is always directed perpendicularly to the velocity. Your pull accelerates the ball into a circular path, but the ball does not speed up or slow down. Your pull changes only the direction of the velocity but not the magnitude of the velocity. If your pull were not perpendicular to the velocity, a component of the acceleration in the direction of the ball's motion would exist and the speed of the ball would change.
In this example, the acceleration is directed toward the center of a circle. Acceleration directed toward a central point is called centripetal acceleration. (The word centripetal means "directed toward a center.")
This example can also be analyzed by means of velocity vectors. Even though the speed of the ball in its circular path is uniform, the velocity is constantly changing. In Figure 5-5(A), A and B represent two successive positions of an object moving with uniform circular motion about point O. The velocity vector vi indicates the velocity of the object when at point A, and the velocity vector vf indicates its velocity at point B. The velocity vectors, vi and vf, are tangent to the circle at A and B respectively, and are thus perpendicular to the respective radii OA and OB.
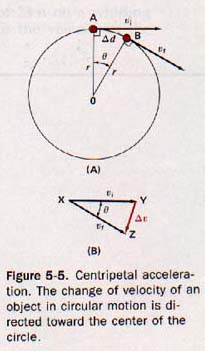
In order to study the change of velocity between vi and vf , a separate vector diagram, Figure 5-5(B), is drawn in which vi and vf originate at point X. If vf is considered the resultant and vi one of its components, then Dv is the other component. This vector Dv represents the change in velocity between vi and vf. Because the vectors vi and vf are equal in magnitude and are perpendicular to their respective radii, The triangles are similar.
Centripetal Acceleration Centripetal Acceleration is the center-seeking force. This is gravity for planets and satellites, or the force on a rope swinging a mass in a circle.
Centrifugal Force The Centrifugal Effect is the attempt of a mass in circular motion to take off tangentially and pursue a straight line by the law of inertia.
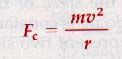
Where Fc is the centripetal force in newtons, m is the mass in kilograms, r is the radius in meters, and v is the velocity in meters/second.
Orbits An orbit is the resultant of the balance between centripetal acceleration and the centrifugal effect.
Critical Velocity Satellites in circular orbit around a planet move with critical velocity. This is the velocity at which the force of gravity on the satellite balances the centrifugal effect of circular motion.
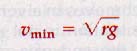
Where vmin is the critical velocity in meters/sec, r is the radius in meters, and g is the acceleration of gravity in m/s2 (9.8m/s2).
5.4 Frames of Reference Consider the NASA centrifuge, a chamber attached to the end of a long boom. The boom is designed to turn around a central point under the observation booth at the top of the picture. (James Bond almost died in one of these).

In operation, the chamber moves at constant speed in a large circle around the central point. Suppose you are in the chamber while it is moving. You would still feel the pull of gravity. In addition, you would feel your body being pressed against the outside wall of the chamber.
You would also observe that a ball placed on the floor would move across the floor toward the outside wall of the chamber. If you drop an object in the chamber, you would see it fall to the floor in a curved path.
From these observations it would seem that Newton's law of inertia does not hold true in the moving chamber. These observations can be explained, however, by attributing them to a force that tends to move all particles toward the outside wall of the moving chamber.
This force moves the ball across the floor and accelerates the falling object so that its path is curved. A force that tends to move the particles of a spinning object away from the spin axis is called centrifugal force. Centrifugal force exists only for an observer in an accelerating system who is considered to be stationary.
An observer in the booth above the moving chamber interprets the situation quite differently, however. To this observer, the chamber and its occupant tend to continue their motion in a straight line because of their inertia.
A force along the boom, a centripetal force, causes the chamber to follow a circular path. And a force exerted by the wall of the chamber on its occupant causes the occupant also to follow a circular path. The observer in the booth can explain the behavior of objects in the chamber in terms of inertia and centripetal force. To this observer, no centrifugal force is involved.
To resolve this seeming contradiction, it is helpful to discuss this situation in terms of frames of reference. Each observer assumes that some surrounding objects are stationary because they do not move with respect to each other.
To the observer in the moving chamber, the walls and fioor of the chamber are stationary and are used as the basis of measurements. Other objects, such as the ball on the floor, move with respect to these stationary objects. The walls and floor of the chamber are the basis for this observer's frame of reference.
A frame of reference is a system for describing the Iocation of objects. It is used to specify the positions and relative motions of objects. A frame of reference in which Newton's first law holds true is called an inertial frame. An accelerating frame of reference is noninertial because Newton's first law does not hold true therein.
The observer in the booth is stationary with respect to the earth. Strictly speaking, however, a frame of reference based on the earth is not an inertial frame. The earth spins and orbits around the sun and describes continuous acceleration in doing so. However, the earth is so close to being an inertial frame that we can consider a frame of reference based on the booth as an inertial frame. (For practical purposes, we often neglect the accelerations of frames of reference that are stationary with respect to the earth.)
The direction of motion of the moving chamber is continually changing. With respect to the observer in the booth, the moving chamber is accelerating. It is, therefore, a noninertial frame. Using such a frame, one can observe acceleration that is not attributed to such forces as friction or gravitation. The concept of centrifugal force is necessary. Centrifugal force is sometimes called fictitious because it is not involved when we decide to use an inertial frame to describe motion.
ROTARY MOTION
5.5 Motion Around an Axis Rotary motion is the motion a body about an internal axis. Rotary motion occurs in a spinning bicycle wheel, the spinning crankshaft of an automobile engine, and a wheel attached to the spinning shaft of an electric motor.
Note the difference between circular motion and rotary motion. In circular motion, the axis of the motion is outside the object. In rotary motion, the axis of the motion is inside the moving object. A spinning wheel is in rotary motion; an object on the rim of the wheel describes circular motion.
For rotary motion to be uniform, the object must spin about a fixed axis at a constant rate. The movement of the hands of a clock is an example of uniform rotary motion. If either the direction of the axis or the rate of spin varies, the rotary motion is variable. The movements of automobile wheels as a car is driven at different speeds and the movements of a spinning top as it slows down are examples of variable rotary motion.
5.6 Angular Velocity For uniform linear motion, velocity is defined as the time rate of displacement. Similarly, for uniform rotary motion, angular velocity is defined as the time rate of angular displacement. Angular displacement is the angle about the axis of rotation through which the object turns. The symbol for angular velocity is the Greek letter omega. The equation for angular velocity is

An angle of one radian is the angle that, when placed with its vertex at the center of a circle, subtends on the circumference an arc equal in length to the radius of the circle.
Since the circumference of a circle is 2π times the radius
1 revolution = 360o = 2π radians
1 radian = 57.3o
Since an angle measured in radians equals the ratio of the length of the subtended arc to the length of the radius, the units cancel, and the angle in radians is a pure number.
The concept of angular velocity includes both the rate of rotation and the direction of the axis of rotation. Angular velocity is a vector quantity represented by a vector along the axis of rotation.
The length of the vector indicates the magnitude of the angular velocity. The direction of the vector is the direction in which the thumb of the right hand points when the fingers of the right hand encircle the vector in the direction in which the body is rotating.
5.7 Angular Acceleration From the study of linear motion we know that a change of velocity defines acceleration. The same is true for rotary motion. Changing either the rate of rotation or the direction of the axis involves a change of angular velocity and thus defines angular acceleration. The uniform rate of change of linear velocity is known as linear acceleration (Section 3.5).
Similarly, the uniform rate of change of angular velocity is known as angular acceleration and designated as alpha, α.


5.8 Rotational Inertia A wheel mounted on a shaft will not start to spin unless a torque is applied to the wheel. A wheel that is spinning will continue to spin at constant angular velocity unless a torque acts on it. In both cases the wheel is in equilibrium. Thus if we replace "force" with "torque," Newton's law of inertia also applies to rotary motion.
If we wish to change the rate of rotation of an object about an axis-- that is, change its angular velocity-- we must apply a torque about the axis. The angular acceleration that this torque produces depends on the mass of the rotating object and upon the distribution of its mass with respect to the axis of rotation.
In Figure 5-10 two masses, ml and m2, are mounted on a bar that is fastened to an axle. The masses can be placed on the bar at varying distances from the axle. If a cord is wound around the axle and attached to a weight that falls under the influence of gravity, a constant torque is applied to the axle.
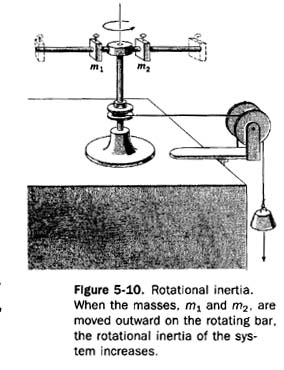
If different weights are attached to the cord, different torques are applied. If the masses mounted on the bar remain in a fixed position, the greater the torque, the greater will be the angular acceleration. If the masses are placed near the axis of rotation, the acceleration produced by a given torque is greater than if they are placed at the ends of the bar.
Moving the masses farther apart does not change the amount of mass that is rotated. It does, however, change the distribution of mass. We say that it increases the rotational inertia. Rotational inertia is the resistance of a rotating object to changes in its angular velocity. The angular acceleration, alpha, is directly proportional to the torque, T, but inversely proportional to the rotational inertia, I

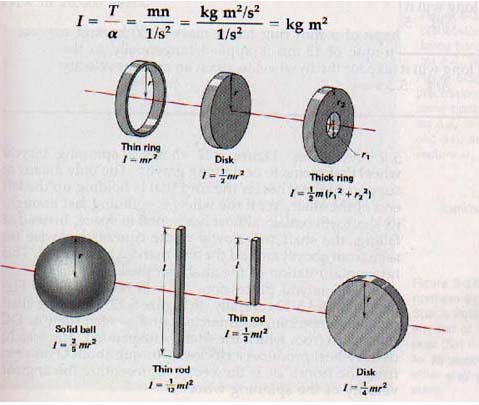
Rotational inertia takes into account both the shape and the mass of the rotating object. Equations for the rotational inertia of certain regularly shaped bodies are given in Figure 5-11. Rotational inertia has the unit dimensions kg.m2.
Figure 5-11
5.9 Precession Figure 5-12 shows a spinning bicycle wheel that seems to be defying gravity. The only means of support of the wheel is the cord that is holding up the left end of the shaft. Yet if the wheel is spinning fast enough, its shaft will remain almost horizontal in space. Instead of falling, the shaft will slowly rotate counterclockwise (as seen from above) around the axis marked by the cord. This horizontal rotation of the shaft is called precession.
To understand precession, we will need to see Figures 5-12. In Figure 5-12, OA is the shaft of a wheel spinning counterclockwise as seen from A. OC is the cord from which the shaft is suspended. The weight of the wheel produces a clockwise torque about O (as seen from the front), is the vector representing the angular velocity of the spinning wheel.
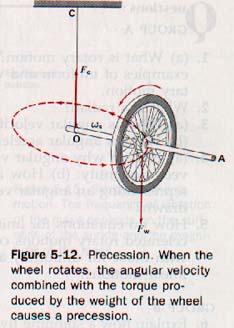
Because of this angular acceleration there will be a change in the angular velocity. This added vectorially to omega results in a new angular velocity of the same magnitude but different direction.
(Remember that the angular acceleration is small and can therefore be considered to be at right angles to both the initial and new angular velocities.) Because of the way the wheel is supported, the shaft of the wheel has to turn toward this new position. The analysis has to be repeated for successive time intervals and the result is the precessional motion of the wheel.
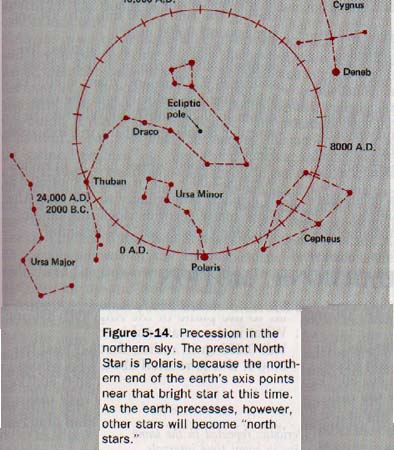
The motion of the earth is a good example of precession since it spins about an axis that is tilted with respect to its plane of revolution around the sun. The rotation of the earth produces an equatorial bulge. The gravitational pull of the sun on the part of the bulge closest to the sun is stronger than the pull on the part of the bulge on the other side of the earth.
Because of the resulting torque, the earth's axis goes through a precessional motion and does not point continually at the same place in space. See Figure 5-14. The earth's axis completes a single precessional cycle in 26,000 years. We will soon need a new "North Star".
5.10 Periodic Motion When a body moves repeatedly over the same path in equal intervals of time, it is said to have periodic motion. Consider a mass attached to a spring that is supported from a horizontal beam. If we pull down on the mass and then let it go, it will vibrate up and down in periodic motion.
If we exert a force, F, acting downward on the mass, we displace it from its equilibrium position by a distance d. We also find by experiment that if we exert a force 2F we displace the mass a distance 2d. The downward displacement from the equilibrium position is directly proportional to the downward force we exert. This is the principle of the spring balance described in Section 1.8.
In exerting this force downward we pull against the spring, and the spring also pulls against our hand with a force F (law of interaction). When we release the mass (A), the upward force of the spring exceeds the downward pull of gravity on the mass, An upward acceleration that is directly proportional to the excess force is produced (law of acceleration).
As the mass returns to its equilibrium position (B), less and less force is exerted on it by the spring. Consequently the acceleration becomes less. The net force is zero when the mass is at its equilibrium position. The acceleration is also zero. The mass has acquired its maximum velocity at this point. It moves past its equilibrium position because of its inertia. As this overshoot occurs, the upward pull of the spring becomes less than the downward force on the mass.
There is a net downward force on the mass, and this downward force decelerates it. The mass stops (C). (During the upward movement of the mass, the spring's pull may change to a downward force due to compression.) The downward force then accelerates it again (D and E).
As a consequence of the upward force exerted by the spring and the downward force due to gravity, the mass describes an up-and-down motion.
Assuming the ideal conditions of a frictionless spring, the mass moves above the equilibrium position the same distance it moves below the equilibrium position, and it completes each up-and-down cycle in the same amount of time. At each point in the up-and-down cycle, the force exerted on the mass, and therefore the resulting acceleration, are directly proportional to the displacement of the mass from the equiiibrium position.
Both the force and the acceleration are directed toward the equilibrium position. The type of periodic motion that has these characteristics is called simple harmonic motion.
Simple harmonic motion is linear motion in which the acceleration is proportional to the displacement from an equilibrium position and is directed toward that position.
5.2 Analyzing Harmonic Motion Simple harmonic motion can be analyzed in terms of circular motion. Consider a light is shining directly down on a rotating wheel. As the wheel spins, the handle on the wheel describes circular motion. The shadow of the wheel and handle falls perpendicularly on the horizontal surface below.
The shadow of the handle moves back and forth along the shadow of the wheel. The shadow of the handle slows down when it is going away from the center of the wheel's shadow and speeds up when it approaches the center point. In other words, the handle's shadow describes simple harmonic motion.
The period is the time of one complete vibration-- the time required for the point to make one revolution on the reference circle. As we saw in Section 1.8, the frequency of a vibratory motion is the number of vibrations per second-- the number of revolutions per second of a point on the reference circle. The frequency is the reciprocal of the period.
5.2 The Pendulum An object suspended so that it can swing back and forth about an axis is called a pendulum.
The mass of the cord is negligible in comparison to the mass of the bob. If the displacement of the bob is small in comparison to the length of the cord, the motion of a pendulum very closely approximates simple harmonic motion.
As the pendulum bob moves from A to B and back again to A, it makes a complete vibration. C is the equilibrium position.
Galileo was probably the first scientist to make quantitative studies of the motion of a pendulum. It is said that he observed the gentle swaying of a sanctuary lamp in the Cathedral at Pisa. Using his pulse as a timer, he found that successive vibrations of the chandelier were made in equal lengths of time, regardless of the amplitude of the vibrations.
He later verified his observations experimentally and then suggested that a pendulum be used to time the pulse rates of medical patients.
In the simple pendulum, all the mass may be considered to be concentrated in the bob. For an ideal pendulum of this type, the following statements hold true:
The Laws of the Pendulum:
1. The period of a pendulum is independent of the mass or material of the pendulum. This statement is strictly true only if the pendulum vibrates in a vacuum. Air resistance has more effect on a pendulum bob made of cotton than it does on a bob made of lead.
2. The period of a pendulum is independent of the amplitude. if the arc is small, the arc is considered small if 10o or less.
3. The period of a pendulum is directly proportional to the square root of its length. If we have a pendulum 25 cm long and one 100 cm long, the period of the longer pendulum will be twice that of the shorter one. Since the square roots of 25 and 100 are 5 and 10 respectively, the periods are in the ratio of 5 to 10, or 1 to 2.
4. The period of a pendulum is inversely proportional to the square root of the acceleration of free fall. Because the earth has an equatorial bulge, a pendulum vibrates slightly faster at the poles than at the equator. If we use the letter l to denote the length of a pendulum and g to denote the acceleration due to gravity, the period, T, is
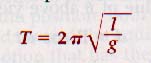
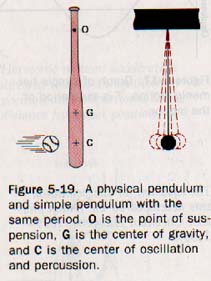
Any real object that can vibrate like a pendulum is called a physical pendulum, as distinguished from a theoretical simple pendulum. For example, a baseball bat can be a physical pendulum as shown in Figure 5-19. When the bat is suspended from O, which is called the center of suspension, and set in vibration, its period will be the same as that of a simple pendulum with a length equal to the distance OC.
Consequently, C is called the center of oscillation. O and C are interchangeable; that is, if the bat is suspended from C, the center of oscillation will be at O. (G is the center of gravity of the bat.)
An additional property of C is that it is the center of percussion of the bat. The batter's hands do not experience a "sting" if a ball strikes the bat at the center of percussion as the hands turn the bat about the center of suspension. If the ball hits the bat at a point other than the center of percussion, the bat rotates about some point other than the center of suspension. The part of the bat at the center of suspension then pushes against the hands, which accounts for the "sting."
SUMMARY
Uniform circular motion is motion at constant speed along a curved path of constant radius. An object moving in a curved path undergoes centripetal acceleration. Centripetal acceleration is produced by a force known as centripetal force which is directed toward a central point.
When gravity is acting on an object, a minimum velocity is required to keep the object moving in a vertical circle. A frame of reference is a system for specifying precisely the location of objects. Centrifugal forces are required to explain the curved motions of objects in terms of a noninertial, or accelerating, frame of reference.
Rotary motion is the motion of a body about an internal axis. In such motion, the relationships among angular displacement, velocity, acceleration, and time are similar to the corresponding relationships for linear motion.
The angular acceleration of a rotating body is directly proportional to the torque that produces motion and inversely proportional to the body's rotational inertia. The rotation of the shaft of a rotating body that is under the influence of gravity is called precession.
Periodic motion occurs when a body continually moves back and forth over a definite path in equal intervals of time. Simple harmonic motion is a special type of periodic motion. Simple harmonic motion can be analyzed in terms of circular motion. A swinging pendulum describes simple harmonic motion.
The period of a pendulum is directly proportional to the square root of its length and inversely proportional to the square root of the acceleration of gravity.
VOCABULARY
angular acceleration, angular velocity, centrifugal force, centripetal acceleration, centripetal force, circular motion, critical velocity, frame of reference, pendulum, periodic motion, precession, radian, rotary motion, rotational inertia, simple harmonic motion.
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester