Velocity and Acceleration

Velocity and Acceleration

The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).
This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.
VELOCITY AND ACCELERATION
3.1 The Nature of Motion If you see a car in front of your house and later see it farther along the street, you are correct in assuming that the car has moved. To reach this conclusion, you observed two positions of the car and you also noted the passage of time. You might not know how the car got from one position to the other. It might have moved at a steady rate or it might have speeded up and then slowed down before it got to its second position.
It might also have been moving when you first noticed it and might still have been moving at its second location. The car may have moved from one location to the other in a straight line, or it may not have. But none of these possibilities changes the truth of the statement that the car has moved.
Usually, when we see something move, we do not just make two observations. We observe the moving object continuously. However, even a case of continuous observation can be thought of as a series of observations in which the interval of time between two successive observations is small.
Figure 3-1 shows several important things about the nature of motion. First, it shows the changing positions of a moving object. Such a change of position in a particular direction is called a displacement. A displacement has magnitude, direction, and a point of origin. A displacement is always a straight line segment from one point to another point, even though the actual path of the moving object between the two points is curved. Furthermore, displacements are vector quantities and can be combined like other vector quantities.
For example, the statement that an airplane flew 500 kilometers south from Chicago describes the airplane's displacement, since the statement specifies the point of origin, magnitude, and direction. Whether the airplane flew in a straight line or not, the airplane's displacement vector is a straight arrow directed south from Chicago and representing a magnitude of 500 kilometers.
Relative motion can be detected by comparing the displacement of one object with respect to another. The reference object is usually considered to be stationary. Thus in the case of the moving car, the street and houses are the stationary references. So motion may be defined as the displacement of an object in relation to objects that are considered to be stationary. This chapter deals with the simplest type of motion the motion of an object along a straight line. Motion in a curved line will be discussed in Chapter 5
3.2 Speed The time rate of motion is called speed. For example, if you are walking at a speed of 3.0 m/s, in 1.0 second you travel 3.0 meters. In 2.0 seconds, you travel 6.0 meters, and in 3.0 seconds you travel 9.0 meters.
A graph of this motion, and of several other motions with constant speeds, is shown in Figure 3-2.
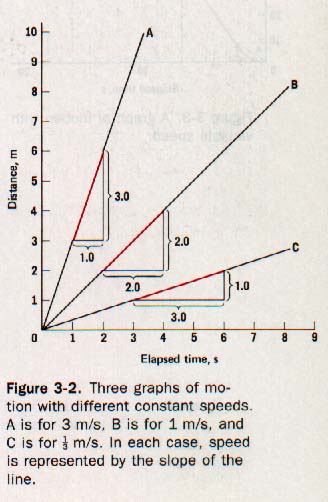
Notice that the lines that represent greater speeds are more steeply inclined. The slope of a line indicates how steep the line is. The slope is the ratio of the vertical component of a line to the corresponding horizontal component. For example, the red segment in line A has a vertical component of 3.0 units and a horizontal component of 1.0 unit. The slope of the 3.0 line is
3.0/1.0 = 3.0
This definition of the slope of a line on a graph may be used to represent a physical quantity such as speed. If the vertical axis represents distance and the horizontal axis represents elapsed time, then the slope of the line represents speed. For each of the speeds graphed in Figure 3-2 the data for computing the slope are given.
A graph such as this and a single computation of the slope will determine the speed over the entire motion only if the speed is constant. If the determination of speed over any randomly chosen interval gives the same value, the speed is constant. The graph of constant speed is a straight line.
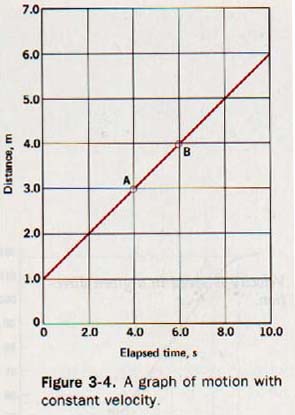
Average speed is found by dividing the total distance by the elapsed time. For example, if you run 112 m in 20.0 s, you might not run at constant speed. You might speed up and slow down. But as long as you move a total distance of 112 m in 20.0 s, your average speed is 5.60 m/s.
Suppose you ride a bicycle 120 m in 20s. Your average speed is
120m/20s = 6.0 m/s.
A graph of your speed may not be a straight line. You start at a speed of 0.0 m/s and increase your speed. Then from about 3 s to 15 s you travel at constant speed. Then at about 16 s you begin to tire and slow down until at 20 s you stop.
Instantaneous speed is the slope of the line that is tangent to the curve at a given point.
Without a speedometer it is difficult to determine your instantaneous speed. It is the speed that you would have if your speed did not change from that point on. Instantaneous speed can be measured approximately by timing the motion over a short distance. .
This method gives only an approximation of the instantaneous speed because we found the average speed for the time interval indicated. This value for the average speed is the same as the instantaneous speed (the slope of the tangent line) at some point in, but we cannot precisely determine that point.
Both instantaneous speed and average speed are completely described in terms of magnitude alone. Hence speed is a scalar quantity.
3.3 Velocity When both speed and direction are specified for the motion, the term velocity is used. In other words, velocity is speed in a particular direction. A person walking eastward does not have the same velocity as a person walking northward, even though their speeds are the same.
Two persons also have different velocities if they walk in the same direction at different speeds. As stated in Section 2.11, velocities are vector quantities. Magnitude and direction are necessary to describe velocities.
For the problems in this chapter, in which the motion is along a straight line, the word "velocity" and the symbol for velocity will be used without stating the direction angle. The values given for velocity will indicate only the magnitude and not the direction.
In these cases the velocity may be either a positive or a negative number to indicate in which direction the object is moving. A negative sign as part of velocity, therefore, does not mean that the speed is negative; speed always represents the magnitude of the velocity. Hence, when the direction angle of velocity is not given, the equations for velocity and speed appear the same.
Average velocity is defined as the total displacement divided by the total elapsed time.
vav = d/t
where vav is the average velocity, d is the change in position is the change in time.
Graphic representations of the velocity of motion along a straight line are shown in Figure 3-4 and Figure 3-5. These graphs indicate that the direction of motion does not change in either case because the magnitude of displacement is continuously increasing, Furthermore, since the graphs do not show the direction of motion, they have the same form as the speed graphs in Figure 3-2 and Figure 3-3. In Figure 3-4.
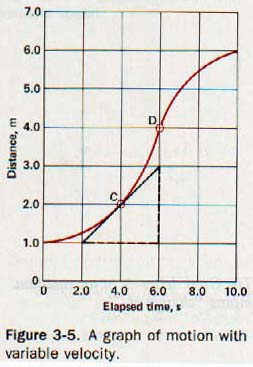
Now suppose we wish to find the velocity at a specific point on the graph, such as point C. To do this, we draw a tangent to the line at C and measure the slope of the tangent. The slope is O.5 m/s, the velocity at C. The velocity at a specific instant in variable motion is called instantaneous velocity to distinguish it from average velocity. The reason that the slope method can be used to measure instantaneous velocity at a specific point on a curved line (just as it was used to measure instantaneous speed in the previous section) is that a very small segment of a curve is almost identical to a straight line segment.
This becomes apparent when you look at the area around point C in Figure 3-5 and imagine it to be magnified 100 times. The red and black line segments near C would then virtually coincide.
Instantaneous velocity is an important concept in variable motion because it enables you to calculate the velocity of a moving object if its motion should stop changing at any point.
3.4 Solving Velocity Vector Problems As vector quantities, velocities can be combined by the parallelogram method discussed in Section 2.11.
ACCELERATION
3.5 The Nature of Acceleration The gas pedal of a car is sometimes called the accelerator. When you drive a car along a level highway increase the pressure on the accelerator, the speed of the car increases. The needle of the car's speedometer shows that for a certain amount of time the car's speed increases. We say that the car is accelerating.
When you apply the brakes of the car that you are driving, the speed of the car decreases. The speedometer indicates that the car's speed is decreasing, and we say that the car is decelerating.
Acceleration is defined as the time rate of change af velocity. An automobile that goes from 0.0 km/hr to 60 km/hr in l0 seconds has greater acceleration than a car that goes from 0.0 km/hr to 60 km/hr in 15 seconds. The first car has an average acceleration of
60 km/hr/10 s = 6.0 (km/hr)/s.
The second car has an average acceleration of 4.0 (km/hr)/s. Acceleration, like velocity, is a vector quantity.
In the case of a car moving along a straight road, acceleration can be represented by a vector in the direction the car is moving. Deceleration occurs in the opposite direction. For the cases in which the motion is known to be along a straight line, the direction of the acceleration is described as positive or negative. In Section 3.3 we saw that the equations for speed and velocity appear the same, since the equations do not specify the direction of displacement. For the same reason, the equations for rate of change of speed and acceleration appear the same. These equations involve only the magnitude and not the direction of the motion.
Average acceleration is found by the relationship
aav = v/t
where aav is the average acceleration, v is the velocity and t is the elapsed time This relationship may also be stated
If the velocity curve is a straight line. the acceleration is a constant. This is an illustration of uniformly accelerated motion.
The dimensions of acceleration should be carefully examined. Acceleration is the rate of change of the rate of displacement, it is in meters and t is in seconds,
acceleration is given in m/s/s, or m/s2.
3.6 Solving Acceleration Problems Galileo Galilei (1564-1642) was the first scientist to understand clearly the concept of acceleration. He found that the acceleration of a ball rolling down an inclined plane and the acceleration of a falling object were both examples of the same natural phenomenon and were described by the same mathematical rules.
Let us consider one of Galileo's experiments. One end of a board is raised so that it is just steep enough to allow a ball to roll from rest to the 0.5-m position in the first second. The apparatus is shown in Figure 3-11. As the ball rolls down the board, its position is shown at one-second intervals.

The data show that the velocity at the end of each second is 1.0 m/s greater than at the end of the previous second. Thus the acceleration is 1.0 (m/s)/s, or 1.0 m/s2. The motion of a ball rolling down an inclined plane is an example of uniformly accelerated motion.
Galileo's experiment verified the property of inertia.
Galileo was among the first scientists to use experiments in testing hypotheses .
The initial velocity of the ball is zero. Its acceleration, or rate of gain in velocity, is 1.0 m/s2.
Therefore its velocity at the end of the first second is 1.0 m/s. (If the ball at that instant were no longer accelerated, it would continue to move with a constant velocity of 1.0 m/s.)
At the end of the next second, its velocity is 2.0 m/s. (2.0 s x 1.0 m/s2 = 2.0 m/s.)
Similarly the ball's velocity at the end of the fifth second is 5.0 m/s.
These data show that the final velocity of an object starting from rest and accelerating at a uniform rate equals the product of the acceleration and the elapsed time. If an object does not start from rest, its final velocity will equal the sum of its initial velocity and the increase in velocity produced by the acceleration.
We may arrive at this same conclusion by mathematical reasoning. The equations are

3.7 Freely Falling Bodies In New York City if a body falls freely from rest, it reaches a velocity of 9.803 m/s in one second of time. We must consider the location because the value of the acceleration depends on the earth's gravity at that location. Since the gravity on the earth may vary from place to place, the value of the acceleration may also vary. (The nature of gravity will be discussed more fully in Sections 3.11-3.13.) A rounded value of 9.80 m/s2 is approximately valid for locations in the United States.
The equations for accelerated motion apply to freely falling bodies. Since the acceleration due to gravity, g, is the same for all objects at a given location, we may substitute g for a in these equations. Thus
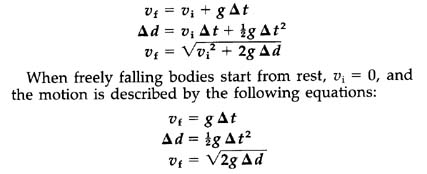
In the case of free-falling bodies, d is always a vertical distance. The vector quantities v and h in these equations are customarily assigned plus signs if they are directed downward and minus signs if they are directed upward.
(The description of the motion is simplified by considering the downward direction of gravity as positive.) These equations apply only to objects that are falling freely in a vacuum because they do not take into consideration the resistance of air, as illustrated in Figure 3-12. These equations do not apply to objects whose air resistance is great compared to their mass, such as leaves falling in air.

An object thrown upward is uniformly decelerated by the force of gravity until it finally stops rising. Then as the object falls, it is uniformly accelerated by the force of gravity.
If the effect of the atmosphere is neglected, then the time required for the object to fall is the same as the time required for it to rise.
NEWTON'S LAWS OF MOTION
3.8 Law of Inertia Thus far in Chapter 3, we have discussed motion apart from its causes. Now we shall study the effects that forces have on motion.
A force is a physical quantity that can affect the motion of an object. A push or a pull is a force. Since a force has magnitude, direction, and a point of application, it is a vector quantity.
The relationships among force, mass, and motion were described clearly for the first time by Sir Isaac Newton (1642-1727) in three laws of motion that bear his name. While some aspects of Newton's laws of motion can be tested only under carefully controlled conditions, repeated experiments and observations have led scientists to believe that the laws are universally true. That is, the laws apply not only to objects on or near the earth, but to objects throughout the universe.
Newton's first law of motion deals with the motion of a body on which no net force is acting. That is, either there is no force at all acting on the body or the vector sum of all forces acting on the body is zero. The word "net" refers to the second situation. Even though a body may have many forces acting on it, these forces may act against each other. They may balance each other in such a way that the body does not change its state of motion.
If such a body is at rest, it will remain at rest. If it is in motion, it will continue in its motion in a straight line with uniform speed.
Newton's first law of motion may therefore be stated as follows:
If there is no net force acting on a body, it will continue in its state of rest or will continue moving along a straight line with uniform velocity.
As we saw in Section 1.8, this property of a body that opposes any change in its state of motion is called inertia. Hence Newton's first law of motion is known as the law of inertia.
At first glance, this law seems to contradict our everyday experiences. If a car is to be kept moving with a constant velocity, the car's engine must apply a constant force to it. If the engine stops applying this force, the car comes to a stop. Only then does the car seem to obey the part of Newton's law that states that objects at rest will remain at rest unless acted upon by an unbalanced force.
Close study of a moving car shows, however, that it is the force of friction that brings the car to a stop and not the absence of the force provided by the engine. If it were possible to remove this friction, it would be reasonable to assume that the car would keep rolling without applying a constant force.
This is, in fact, what happens in space travel. Once a spaceship is beyond the pull of the earth's gravity, it continues to move with constant velocity even without the thrust of its engines.
The study of the motion of a car in the absence of friction is an example of a thought experiment since the study cannot be performed under actual conditions. It was a thought experiment of this kind that led Galileo to an understanding of inertia even before Newton described it. Galileo noticed that if a ball rolls down one incline and up a second one, the ball will reach almost the same height on the second incline as the height from which it started on the first incline.
Galileo concluded that the difference in height is caused by friction and that if friction could be eliminated the heights would be exactly alike. Then he reasoned that the ball would reach the same height no matter how shallow the slope of the second incline. Finally, if the second slope were eliminated altogether, the ball would keep rolling indefinitely with constant velocity.
This is the same idea as the one expressed in Newton's first law of motion. Inertia keeps a stationary object stationary and a moving object moving. The greater the mass (and inertia) of an object, the greater is the force required to produce a given acceleration. A pencil lying on the floor has relatively little mass and therefore little inertia. You can produce acceleration easily by kicking it with your foot. A brick has much more mass and more inertia. You can easily tell its difference from the pencil if you kick it.
Newton's first law specifies which forms of motion have a cause and which forms do not. Uniform motion in a straight line is the only motion possible for an object far removed from other objects. Nonuniform motion is always caused by the presence of some other object.
3.9 Law of Acceleration Newton's first law of motion tells us how a body acts when there is no net applied force. Let us consider what happens when there is either a single applied force or two or more applied forces whose vector sum is not zero. (Forces are vector quantities since they have direction as well as magnitude.)
In the following discussion, we shall use "applied force" or just "force" to mean the vector sum of all forces applied to the body. Newton's second law of motion states: The effect of an applied force is to cause the body to accelerate in the direction of the force. The acceleration is in direct proportion to the force and in inverse proportion to the mass of the body.
If the body is at rest when the force is applied, it will begin to move in the direction of the force and will move faster and faster as long as the force continues.
If the body is moving in a straight line and a force is applied in the direction of its motion, it will increase in speed and continue to do so as long as the force continues. If the force is applied in the direction opposite to the motion, the acceleration will again be in the direction of the force, causing the body to slow down. If such a force continues long enough, the body will slow down to a stop and then begin to move with increasing speed in the opposite direction.
If the force applied to a moving object is not along the line of its motion, the acceleration will still be in the direction of the force. The effect in general will be to change both the direction and the speed of the motion. We shall postpone detailed consideration of this more complex case until Chapter 5. For the present we shall consider only the speed of an object initially at rest or one that is moving in a straight line that is changed only by a force acting along that line.
It should be emphasized again that a body to which no force is applied has zero acceleration. If such a body is in motion, its velocity does not change. If it is at rest, its velocity remains unchanged; its velocity stays at zero. And when there is no change in velocity, the acceleration is zero. When a force is applied to a body, the acceleration is not zero, the velocity changes, and the acceleration is in the direction of the applied force.
If different forces are applied to the same body, the magnitude of the acceleration is directly proportional to the amount of the force. That is, doubling the force causes the acceleration to double, and so on.
We can express such a direct proportion as an equation by saying that one of the quantities equals the other one times a constant, or
F = ka
in which F is the applied force, a is the resulting acceleration, and k is the constant of proportionality. Since F and a are both vectors, this equation also says that the applied force and the resulting acceleration are in the same direction (which is a restatement of the first part of Newton's second law of motion).
What happens when forces are applied to different objects? This question brings us to the third part of Newton's second law. It turns out that the equation F = ka is always true but that the value of k is different for different objects. In fact, we find that if we properly define the units of force and mass, the value of k for any object is identical with the mass, m, of that object. Thus the equation is written
F = ma
In the metric system, the unit of mass is the kilogram and acceleration has the units of meters per second. (See Section 3.5.) The force required to accelerate 1 kilogram of mass at 1 meter per second2 is 1 kg m/s2. This relationship defines the newton in terms of fundamental units. That is,
1 n = 1 kg m/s2
Since F = ma, if the force is that due to gravity which we call weight, then
Fw = mg
where Fw is the weight in newtons, m is the mass in kilograms, and g is the acceleration of gravity, 9.8 m/s2.
Example: Find the weight of the Boom whose mass is 80 kg.
Fw = mg, so Fw = (80kg)(9.8m/s2).
Boom's weight is 784 n.
3.10 Law of Interaction Newton's third law of motion may be stated as follows: When one body exerts a force on another, the second body exerts on the first a force of equal magnitude in the opposite direction.
To illustrate this law, consider some of the forces that are exerted when a book is resting on the top of a level table. The book exerts a downward force against the table. The table top exerts an upward force on the book. These forces are equal in magnitude and opposite in direction.
When you walk forward on a level floor your feet exert a horizontal force against the floor, and the floor pushes against your feet with a force of equal magnitude, but in the opposite direction.
In each of these situations we have two objects. In the first instance, the objects are the book and the table. In the second instance, they are the foot and the floor. Two forces are involved in each situation. In the first, they are the force of the book against the table and the force of the table against the book. In the second, they are the force of the foot against the floor and the force of the floor against the foot.
In cases such as these, one force may be called the action, while the second force may be called the reaction. Unaccompanied forces do not exist in nature. The law of reaction holds true for all objects at all times, whether they are stationary or moving. Every force is resisted by an equal and opposite force, independent of the motion of the objects involved.
Let us consider another example. A boy rows a boat toward the shore of a lake and, when he is a meter or so from shore, he attempts to leap ashore. He exerts a force against the boat and the boat exerts an equal but opposite force against him. The force exerted by the boat against the boy accelerates him.
The direction of his acceleration is opposite to the direction in which his force caused the boat to be accelerated. If we assume the resistance to the motion of the boat by the water to be negligible, the amount of acceleration of each object is inversely proportional to its mass.
The boy might judge the force he must exert to reach shore on the basis of his experience in jumping the same distance from an object fixed on the earth. If so, when he jumps from the boat, he might not reach shore, but instead fall into the water. Splash!
Suppose a kilogram mass is suspended from two spring balances that are connected, as shown in Figure 3-17. As we learned in Section 2.4, a kilogram weighs about 9.8 newtons near the earth's surface. Then why do both balances have a reading of 9.8 newtons?

The answer is Newton's third law. The downward force exerted by the mass is accompanied by an equal upward force exerted by the person's hand. Neither force can exist without the other. If additional balances are added in this experiment, each balance will still read 9.8 newtons (provided the weight of each balance is neglected). Can you explain why?
You may think that motion cannot occur if action and reaction are equal. If two people pull on a lightweight wagon with equal force in opposite directions, the wagon will not move. But this is not an example of action and reaction. There are two forces, it is true, and they have the same magnitude and opposite directions, but they are both exerted on the same object.
Action and reaction apply when forces are exerted on different objects. For example, action and reaction are involved in the force that each one's feet exert against the ground and the equal but opposite force the ground exerts against the feet.
3.11 Newton's Law of Universal Gravitation In addition to formulating his three laws of motion, Newton described the force that makes falling bodies accelerate toward the earth. In doing so, he made use of the laws of planetary motion that were developed by Johannes Kepler almost a century before Newton's time. See Section 1.4.
In Newton's account of his study of falling bodies, he states that he wondered whether the force that makes an apple fall to the ground was related to the force that keeps the planets in their orbits. If so, a single law could be used to describe the attraction between objects in the entire universe.
From Kepler's laws, Newton deduced the fact that the force of attraction between two objects is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between their centers of mass. (The center of mass of an object is that point at which all its mass can be considered to be concentrated. This concept is similar to that of "center of gravity," which will be discussed in Chapter 4.)
Newton called this attractive force the force of gravitation. Hence the statement is known as Newton's law of universal gravitation. In equation form
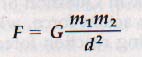
where F is the force of gravitation, ml and m2 are the masses of the attracting objects, d is the distance between their centers of mass, and G is a proportionality constant called the universal gravitational constant.
An example using you on the earth: F is your weight in newtons, m1 is your mass in kilograms, m2 is the mass of the earth in kilograms.
Newton was only able to confirm his theory with astronomical observations. He was unable to measure G with the laboratory instruments available at his time. The first determination of G was made in 1797 by the English scientist Henry Cavendish (1731-1810). A schematic diagram of this experiment is shown in Figure 3-18.
Two small lead spheres are attached to the end of a lightweight rod that has a mirror attached to it. The rod is suspended by a thin quartz fiber. Two large lead spheres are placed in fixed positions near the small spheres.
The gravitational force between the fixed and movable spheres draws the movable spheres toward the fixed ones. This motion causes the suspending fiber to twist. The fiber offers a slight resistance to twisting. The resistance increases as the twisting increases, and the angle of twist is proportional to the force of gravitation between the fixed and the movable spheres.
The angle of twist could be measured directly from the rod's movement, but the sensitivity of the instrument can be increased by shining a light into the mirror. The light is reflected onto a distant scale, and small movements of the mirror result in large movements of the reflected light across the scale.
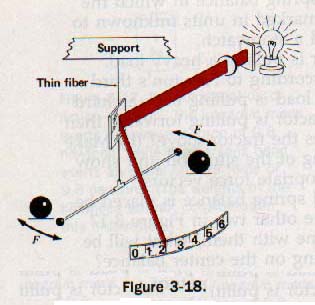
Such an arrangement is called an optical lever. Since G has a very small value, extreme care must be used to isolate the Cavendish apparatus from outside forces such as those produced by air currents and electric charges. The value of G has been found to be 6.67 x 10-11 n.m2/kg2.
3.12 The Mass of the Earth Once G has been measured, the equation for Newton's law of universal gravitation can be used to find the force of gravitation between any two objects of known mass with a known distance between their centers of mass.
Or if the force of gravitation, the distance, and one of the masses are known, the equation can be used to find the value of the other mass. For example, the equation can be used to find the mass of the earth.
In the equation, use me the mass of the earth, for ml, use mp, the mass of a particle on the earth's surface. Newton showed that, for a spherical mass, we can consider all of the mass to be located at the center. So in this case d will be the radius of the earth. The force of gravitation, F, will be the weight of the particle, so we shall replace F by Fw.
Since both G and me, are constants, the acceleration due to gravity in a given location depends only on the square of the distance from the center of the earth.
3.l3 Relation Between Gravity and Weight The term gravity is used to describe the force of gravitation on an object on or near the surface of a celestial body such as the earth. Thus we say that the moon has less gravity than the earth because the force of gravitation near the moon's surface is less than the force of gravitation near the earth's surface.
A calculation of the gravity of a celestial body near the surface must take into consideration the size of the body since the force of gravitation varies inversely with the square of the distance to the center of mass of the body.
The value for the mass of the earth can be used to determine the theoretical value of the gravity at any given location on or above the earth's surface. Such factors as local variations in the composition of the earth's crust and the effect of the earth's rotation must be considered to obtain the actual value of the gravity at a particular location.
The weight of an object is the measure of the force of attraction between the object and the earth. When we say that a person weighs 900 n, we mean that the force exerted on that person by the earth is 900 n.
The person also exerts a force of 900 n on the earth. The weight of an object equals the product of its mass and the acceleration due to gravity. The mass of an object is constant. But the acceleration due to gravity is inversely proportional to the square of the distance from the center of the body to the center of the earth.
All parts of the earth's surface are not the same distance from its center. The variations range from 393 m below sea level at the Shole of the Dead Sea to 8848 m above sea level at the top of Mount Everest.
An object at the top of a mountain, Where gravity is less, will weigh less there than it does at sea level. Also, since the earth is slightly flattened at the poles and since the earth's rotation counteracts the force of gravitation, an object weighs a little more at the North Pole than it does at the equator.
3.l4 Gravitational Fields The value of g, the acceleration due to gravity, at a particular point is sometimes called the gravitational field strength at that point. The effect of rotation, if any, is usually included in determining g. A region of space in which each point is associated with the value of g at that point is called a gravitational field.
Since g is an acceleration, it is a vector. Hence a gravitational field is a region of space in which each point has associated with it a vector equal to the value of g at that point and which is called the gravitational field strength.
If an object of mass m is located at any point in a gravitational field, the force of gravitation on the object can be calculated by the equation in Section 3.9
Fw = mg
If the mass of the object is 1 kg, then F, is numerically equal to g. Another way to think of the gravitational field strength at a point is that it equals the force of gravitation that would be exerted on a mass of one kilogram if the mass were located at that point, or
g = Fw/m
The value of g for the earth varies with the distance from the center of the earth and with certain other aspects of the earth's motion and composition. Vectors are used to represent the gravitational field strength at various altitudes.
The concept of a field is more complex than the idea of forces pushing on objects. Yet the field concept can explain more physical phenomena (such as electromagnetic waves) than can the simpler concept of forces.
The field idea pictures objects as having associated regions such that a mass would be acted on by a force if it were placed in the region. Thus a ball falls to the earth because of interaction between the earth's gravitational field and the ball.
Another way to describe a gravitational field is to say that an object changes the properties of the space in its vicinity. However, the field concept does not explain the cause of gravitation any more than the idea of acceleration does.
Even though scientists are able to express certain aspects of gravitation in terms of acceleration and force fields, the real nature and origin of the force of gravitation are still unknown.
SUMMARY
Displacement is a change of position of an object in a particular direction. Motion is the displacement of an object in relation to stationary objects. Speed is the time rate of change of position (displacement). Velocity is speed in a particular direction. Speed is a scalar quantity, but velocity is a vector quantity.
Graphs can be used to determine average and instantaneous speed and velocity. Velocity problems can be worked either graphically or trigonometrically by use of the parallelogram method of vector addition.
Acceleration is the rate of change of velocity. The relationships among displacement, time, initial and final velocity, and acceleration can be expressed as equations. In the case of freely falling bodies, the acceleration caused by the earth's gravity is used.
A force is a physical quantity that can affect the motion of an object. Newton's laws of motion are
(1) a body will continue in its state of rest or uniform motion in a straight line unless a net force acts on it;
(2) the acceleration of a body is directly proportional to the net force exerted on it, inversely proportional to its mass, and in the same direction as the force;
(3) when one body exerts a force on another body, the second body exerts an equal force on the first body but in the opposite direction.
The force of gravitation is the mutual force of attraction between bodies. Newton's law of universal gravitation states that the force of gravitation between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass.
The mass of the earth can be calculated by means of this law. The force of gravitation near the surface of a celestial body is called gravity. The values of gravity at various distances from a celestial body make up the gravitational field of the body.
VOCABULARY
acceleration, average acceleration, average speed, average velocity, constant speed, constant velocity, displacement, gravitational field, motion, instantaneous speed, slope, instantaneous velocity, speed, law of acceleration, law of inertia, law of interaction, law of universal gravitation, gravity, thought experiment, variable, acceleration, variable speed, variable velocity, velocity
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester