The Nature of Light

The Nature of Light

The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).
This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.
WAVES AND PARTICLES
In 1865, James Clerk Maxwell proposed the electromagnetic theory of light on the basis of extensive mathematical calculations. Twenty years later Heinrich Hertz accidentally discovered radio waves, which verified Maxwell's theory. The metric unit of frequency is named in honor of Hertz.
12.1 Properties of Light The general properties of waves are described in Chapter 10. They are restated and briefly summarized as follows:
1. Propagation within a uniform medium is along straight lines.
2. Refection occurs at the surface, or boundary, of a medium.
3. Refraction, or bending, may occur where a change of speed is experienced.
4. Interference is found where two waves are superposed.
5. Diffraction, or bending around corners, takes place when waves pass the edges of obstructions.
These properties are easily recognized in the behavior of sound and water waves. Such disturbances occur in matter, the particles of the medium being set in motion about their equilibrium positions by the passing waves. Matter is not required for the propagation of light. While light does pass readily through certain kinds of matter, its transmission is unhindered in interstellar space or through an evacuated vessel.
The regular reflection of light from smooth surfaces was known in the time of Plato, almost twenty-four hundred years ago. (Reflection is the subject of Chapter 13.) The refraction of light at the interface (boundary) of two transparent media of different optical densities was observed by the Greeks as early as the second century A.D.
The Arabian mathematician Alhazen (965-1039) studied the refraction of light and disputed the ancient theory that visual rays emanated from the eye. He demonstrated the refractive behavior of light as it passed from one medium into another of greater optical density. See Figure 12-1.

He believed that the angles of incidence and refraction are related, but was unable to determine how they are related. This relationship, now known as Snell's law, was established six hundred years later. (Refraction and Snell's law are discussed in Chapter 14.) The shapes of shadows and the practical use of sight lines for placing objects in a straight line give evidence of the straight-line, or rectilinear, propagation of light. Greek philosophers were familiar with this property of light. Sir Isaac Newton conducted experiments on the separation of light into colors by means of a prism and was aware of the colors produced by thin films.
Rectilinear propagation, reflection, and refraction are the principal light phenomena that were familiar to observers in the seventeenth century. It must have been evident to Newton and his contemporaries that since the transmission of energy from one place to another was involved, only two general theories could explain these properties of light.
In general, energy can be propagated either by particles of matter or by wave disturbances traveling from one place to another. A window pane may be shattered by a moving object, such as a baseball thrown from a distance, or by the concussion ("shock wave") from a distant explosion.
Arguments favoring both a particle (corpuscular) theory and a wave theory were plausible when applied to the properties of light observed in the seventeenth century.
The principal advocate of the corpuscular theory was Newton, whose arguments were supported by the French mathematical physicist and astronomer Laplace (17491827).
The wave theory was upheld principally by Christian Huygens (hi-ganz) (1629-1~95), a Dutch mathematician, physicist, and astronomer. He was supported by Robert Hooke of England.
Because of the plausibility of both theories, a scientific debate concerning the nature of light developed between the followers of Newton and the followers of Huygens and continued unresolved for more than a century. What are some of the arguments that support each of these classical theories of light?
12.2 The Corpuscular Theory Sir Isaac Newton believed that light consists of streams of tiny particles, which he called "corpuscles," emanating from a luminous source. Let us examine the arguments used by those who believed the particle theory best explained the various light phenomena known to them.
1. Rectilinear propagation. A ball thrown into space follows a curved path because of the influence of gravity. Yet if the ball is thrown with greater and greater speed, we know that its path curves less and less. We can easily imagine minute particles traveling at such enormous speed that their paths essentially form straight lines.
Newton experienced no difficulty in explaining the rectilinear propagation of light by means of his particle model. In fact, this property of light provided the supporters of the corpuscular theory with one of their strongest arguments against a wave theory. How, they asked, could waves travel in straight lines? A sound can easily be heard around the corner of an obstruction, but a light certainly cannot be seen from behind an obstruction. The former is unquestionably a wave phenomenon. How can the latter also be one?
The simple and direct explanation provided by the particle model of light, together with the great prestige of Sir Isaac Newton, were largely responsible for the preference shown for the corpuscular theory during the seventeenth and eighteenth centuries.
2. Reflection. Where light is incident on a smooth surface, such as a mirror, we know that it is regularly reflected.
How do particles behave under similar circumstances? Steel ball bearings thrown against a smooth steel plate rebound in much the same way light is reflected. Perfectly elastic particles rebounding from a resilient surface, then, could provide a suitable model for the reflection of light. See Figure 12-2.
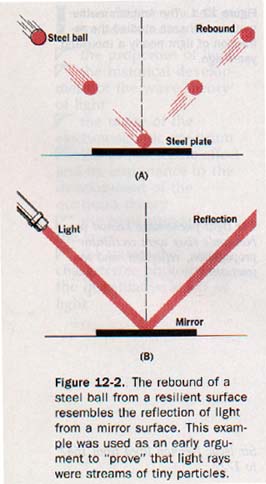
3. Refraction. The corpuscular theory required that the speed of light in water be higher than the speed of light in air. Newton recognized that if it should ever be determined that the speed of light in water is lower than the speed of light in air, his corpuscular theory would have to be abandoned. This uncertainty about the speed of light in water remained unresolved for one hundred twenty-three years after Newton's death. In 1850 the French physicist Jean Foucault (foo-koh) (1819-1868) demonstrated experimentally that the speed of light in water is indeed lower than the speed of light in air. This condition was predicted by the wave theory.
22.3 The Wave Theory Christian Huygens is generally considered to be the founder of the wave theory of light. Although somewhat different in its modern form, Huygens' basic concept is still very useful to us in predicting and interpreting the behavior of light. Let us recall a familiar characteristic of water waves as an introduction to this important principle.
If a stone is dropped into a pool of quiet water, it creates a disturbance in the water and a series of concentric waves travels out from the disturbance point. The stone quickly comes to rest on the bottom of the pool, so its action on the water is of short duration.
However, wave disturbances persist for a considerable time thereafter and cannot reasonably be attributed to any activity on the part of the stone. It must be that the disturbances existing at all points along the wave fronts at one instant of time generate those in existence at the next instant.
Huygens recognized this logical deduction as a basic aspect of wave behavior and devised a geometric method of finding new wave fronts. His concept, published in 1690 and now recognized as Huygens' principle, may be stated as follows: Each point on a wave front may be regarded as a new source of disturbance.
According to this principle, a wave front originating at a source S in Figure 12-4(A) arrives at the position AB. Each point in this wave front may be considered as a secondary source sending out wavelets. Thus from points 1, 2, 3, etc., a series of wavelets develops simultaneously. After a time t these wavelets have a radius equal to vt, where v is the velocity of the wave.
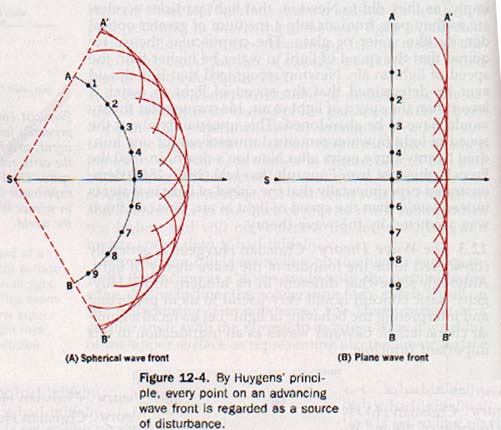
The principle further states that the surface A'B', tangent to all the wavelets, constitutes the new wave front. It is apparent from Figure 12-4 that spherical wave fronts are propagated from spherical wavelets and planar wave fronts from planar wavelets.
The wave theory treats light as a train of waves having wave fronts perpendicular to the paths of the light rays. In contrast to the particle model discussed earlier, the light energy is considered to be distributed uniformly over the advancing wave front. Huygens thought of a ray merely as a line of direction of waves propagated from a light source.
The supporters of the wave theory were able to satisfactorily explain reflection and refraction of light. The explanation of refraction required that the speed of light in optically dense media, such as water and glass, be lower than the speed of light in air. They had trouble, however, explaining rectilinear propagation. This was the primary reason Newton rejected the wave theory.
Before the nineteenth century, interference of light was unknown and the speed of light in such media as water and glass had not been measured.
Diffraction fringes or shadows had been observed as early as the seventeenth century. In the absence of knowledge of interference, however, neither Newton nor Huygens attached much significance to this diffraction phenomenon.
In 1801 the interference of light was discovered. This was followed in 1816 by the explanation of diffraction based on interference principles, as discussed in Chapter 15.
These two phenomena imply a wave character and cannot be satisfactorily explained by the behavior of particles. Thus despite the great prestige of Sir Isaac Newton, the corpuscular theory was largely abandoned in favor of the wave theory.
The final blow to the corpuscular theory came when Foucault found that the speed of light in water was lower than the speed of light in air. Through the remainder of the nineteenth century the wave concept supplied the basic laws from which came remarkable advances in optical theory and technology.
22.4 The Electromagnetic Theory Hot objects transfer heat energy by radiation. If the temperature is high enough, these objects radiate light as well as heat. If a light source is blocked off from an observer, its heating effect is cut off as well. For this reason, a cloud that obscures the sun's light cuts off some of the sun's heat at the same time.
The English physicist Michael Faraday (1791-1867) became concerned with the transfer of another kind of energy while investigating the attraction and repulsion of electrically charged bodies. In 1831 these experiments led him to the principle of the electric generator.
The corpuscular theory was largely abandoned in favor of the wave theory following the discovery of interference and diffraction of light. Note that the speed of light in water had not yet been measured.
Faraday's practical mind required a model to interpret and explain physical phenomena. It was difficult for him to visualize electrically charged objects attracting or repelling each other at some distance with nothing taking place in the intervening space.
Thus he conceived a space under stress and visualized tubes of force between charged bodies. Faraday was not an astute mathematician and so did not put his model for this "transmission of electric force" into abstract mathematical form.
The Scottish mathematical physicist James Clerk Maxwell (1831-1879) set out to determine the properties of a medium that would transmit the energies of heat, light, and electricity. By the year 1865 he had developed a series of mathematical equations from which he predicted that all three are propagated in free space at the speed of light as electromagnetic disturbances.
This unification, the electromagnetic theory, brought into common focus the various phenomena of radiation.
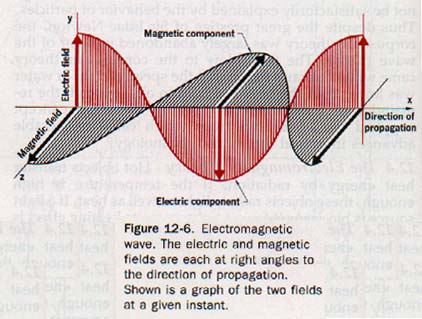
Maxwell determined that the energy of an electromagnetic wave is equally divided between an electric field and a magnetic field, each perpendicular to the other, and both perpendicular to the direction of propagation of the wave.
In Section 10.1 we defined a wave as a periodic disturbance that propagates itself through a medium or space. In this sense, an electromagnetic waves is a periodic disturbance involving electric and magnetic forces. A model of an electromagnetic wave at a given instant is shown in Figure 12-6.
By 1885 experimental confirmation of the electromagnetic theory was achieved by the German physicist Heinrich Rudolf Hertz (1857-1894). Hertz showed that light transmissions and electrically generated waves are of the same nature. Of course, many of their properties are quite different because of great differences in frequency.
Maxwell's theory of electromagnetic waves seemed to provide the final architecture for optical theory; all known optical effects could now be fully explained. Many physicists felt at this time that all the significant laws of physics had been discovered and that there was little left to do other than develop new and more sophisticated techniques for measuring everything more accurately.
In this connection Hertz stated, "The wave theory of light is, from the point of view of human beings, a certainty." Ironically, it was Hertz who was soon to discover a most important phenomenon having to do with the absorption of light energy, one that would create a dilemma involving the wave theory and at the same time set the stage for the new physics that was to emerge in the early years of the twentieth century.
12.5 The Electromagnetic Spectrum Electromagnetic energy can be detected and measured by physical means only when it is intercepted by matter and changed into another form of energy such as thermal, electric, kinetic, potential, or chemical energy.
Today, the electromagnetic spectrum is known to consist of a tremendous range of radiation frequencies extending from about 10 hz to more than 1025 hz. All electromagnetic radiations travel in free space with the constant velocity of 3 x 108 meters per second.
From the wave equation ![]() of Section 10.6, it is evident that the wavelengths (lambda) of these radiations are inverse functions of their respective frequencies (f). Therefore, the range of the electromagnetic spectrum in terms of radiation wavelengths is from about 3 x 107 meters in the low-frequency region to less than 3 x 10-17 meter in the high-frequency region.
of Section 10.6, it is evident that the wavelengths (lambda) of these radiations are inverse functions of their respective frequencies (f). Therefore, the range of the electromagnetic spectrum in terms of radiation wavelengths is from about 3 x 107 meters in the low-frequency region to less than 3 x 10-17 meter in the high-frequency region.
In terms of the angstrom (A), a unit frequently used to express the wavelengths of electromagnetic radiations, the range is from about 3 x 1017 A to 3 x 10-7 A, an angstrom being equal to 10-10 meter.
Eight major regions of the electromagnetic spectrum are commonly recognized. These regions are based on the general character of the radiations. All kinds of electronic transmissions are accommodated in the radio-wave region. Commercial electricity falls within the power region.
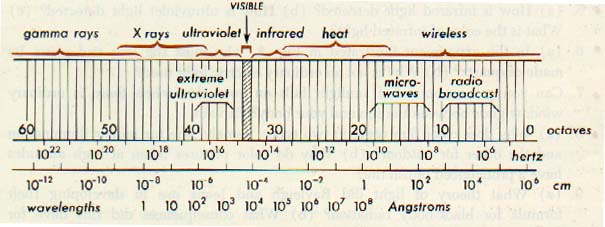
Observe the very small region occupied by the visible spectrum. The optical spectrum includes those radiations, commonly referred to as light, that can be detected visually. Their wave lengths range from approximately 7600 A to 4000 A.
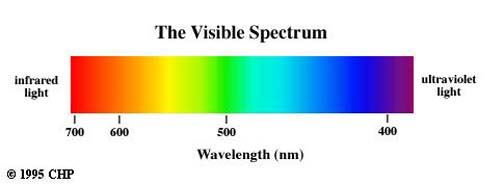
Accordingly, light may be defined as radiant energy that a human observer can see. The optical spectrum also extends into the near infrared and into the near ultraviolet. Although our eyes cannot see these radiations, they can be detected by means of photographic film.
12.6 The Photoelectric Effect As mentioned in Section 12.4, Hertz conducted experiments that led to confirmation of the electromagnetic theory. While studying the radiation characteristics of oscillatory discharges he observed that a spark discharge occurred more readily between two charged spheres when they were illuminated by another spark discharge.
At about the same time, other investigators found that negatively charged zinc plates lost their charge when illuminated by the ultraviolet radiations from an arc lamp. Positively charged plates were not discharged when similarly illuminated.
Observations of the peculiar effects of ultraviolet radiation on metal surfaces led to the discovery of the photoelectric effect, a phenomenon that defied explanation based on the electromagnetic wave theory of light.
Figure 12-10 shows two freshly polished zinc plates A and B that are sealed in an evacuated tube having a quartz window and are connected externally to a battery and galvanometer (a sensitive current-indicating meter).
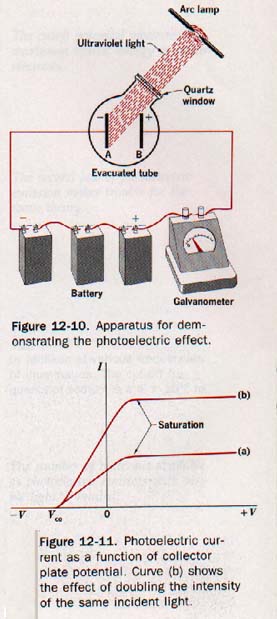
The quartz window transmits ultraviolet radiation, which does riot pass through glass. The galvanometer indicates a small current in the circuit when ultraviolet light falls on the negative plate A.
If a sensitive electrometer circuit is substituted for the battery, it may be shown that the plate exposed to the ultraviolet light acquires a positive charge. The results of these experiments imply that the action of the light on the zinc plate causes it to lose electrons.
The German physicist Philipp Lenard (1862-1947) published the results of the first quantitative studies of the photoelectric phenomenon in 1902. By measuring the charge to mass ratio of the negative electricity derived from an aluminum plate illuminated by ultraviolet light, he was able to prove that electrons were ejected from the metal surface.
Such electrons are called photoelectrons. Subsequent investigations have shown that all substances exhibit photoemission of electrons. The emission of electrons by a substance when illuminated by electromagnetic radiation is known as the photoelectric effect.
12.7 Laws of Photoelectric Emission Plate B of Figure 12-10, having a positive potential V with respect to the emitter plate A, acts as a collector of photoelectrons ejected from the emitter.
If the positive potential is increased enough, all photoelectrons are collected by plate B and the photoelectric current reaches a certain limiting, or saturation, magnitude.
Curve a of Figure 12-11 is a graph of photoelectric current as a function of collector plate potential for a given source of light. Curve b shows the result of doubling the intensity of the light.
Observe that the magnitude of the saturation current is doubled. This means, of course, that the rate of emission of photoelectrons is doubled.
Here we have evidence of the first law of photoelectric emission: The rate of emission of photoelectrons is directly proportional to the intensity of the incident light.
For an electron to escape through the surface of a metal, work must be done against the forces that bind it within the surface. This work is known as the work function.
The photoelectrons must acquire from the incident light radiation the energy needed to overcome this surface barrier. If electrons acquire less energy than the work function of the metal, they cannot be ejected. On the other hand, if they acquire more energy than is required to pass through the surface, the excess appears as kinetic energy and consequently as velocity of the photoelectrons.
We may assume that light penetrates a few atom layers into the metal and that the photoelectric effect will occur at varying depths beneath the surface. Photoelectrons ejected from atom layers below the surface will lose energy through collisions in reaching the surface and must then give up energy equal to the work function of the metal in escaping through the surface.
Photoelectrons ejected from the surface layer of atoms lose only the energy necessary to overcome the surface attractions. Thus in any photoelectric phenomenon we should expect photoelectrons to be emitted at various velocities ranging up to a maximum value possessed by electrons having their origin in the surface layer of atoms.
We can test the logic of these deductions by experimenting further with the photoelectric cell of Figure 12-10. A positive potential of a few volts on the collector plate B produces a saturation current as shown in Figure 12-11. (Above.)
If the collector plate potential is lowered towards zero, the photoelectric current decreases slightly, but at zero potential may still be close to the saturation magnitude.
As the collector plate potential is made slightly negative with respect to the emitter, the photoelectric current decreases also. By increasing this negative potential a value is reached where the photoelectric current drops to zero. This is called the stopping, or cutoff potential V, and is shown in Figure 12-11.
A negative potential on the collector plate repels the photoelectrons, tending to turn them back to the emitter plate. Only those electrons having enough kinetic energy and velocity to overcome this repulsion reach the collector. As the cutoff potential is approached, only those photoelectrons with the highest velocity reach the collector.
These are the electrons with the maximum kinetic energy that are emitted from the surface layer of the metal. At the cutoff potential even these electrons are repelled and turned back to the emitter.
Thus the negative collector potentials, which repel rather than attract photoelectrons, reveal something about the kinetic energy distribution of the ejected electrons. As this potential is made more negative, a nearly linear decrease in photoelectron current shows us that the photoelectrons do have a variety of velocities.
The cutoff potential measures the kinetic energy of the fastest photoelectrons .
From curves a and b shown in Figure 12-11 (above) observe that the photoelectric currents produced by different intensities of incident light from a certain source reach zero at the same collector potential.
Thus the cutoff potential for a given photoelectric system and the velocity of the electrons expelled are independent of the intensity of the light source. From these observations we can formulate a second law of photoelectric emission:
The kinetic energy of photoelectrons is independent of the intensity of the incident light.
The American physicist Robert A. Millikan (1868-1953) performed many experiments with various emitters and light sources. By illuminating emitters made of sodium metal with light radiations of different frequencies, Millikan found that the cutoff potential had different values for the various frequencies of incident light.
By plotting the cutoff potentials V, as a function of light frequencies f, a straight line produced.
Millikan demonstrated that the cutoff potential depends only on the frequency of the incident light.
Recalling that the cutoff potential measures the kinetic energy of the fastest photoelectrons ejected in a particular photoelectric system, we must conclude that the maximum kinetic energy of photoelectrons increases with the frequency of the light illuminating the emitter.
These facts provide us with a third law of photoelectric emission:
Within the region of effective frequencies, the maximum kinetic energy of photoelectrons varies directly with the difference between the frequency of the incident light and the cutoff frequency.
12.8 failures of the Wave Theory The experiments of Hertz, together with those which followed, confirmed that Maxwell's electromagnetic theory correctly describes the transmission of light and other kinds of radiation.
This wave theory requires the radiated energy to be distributed uniformly and continuously over a wave front. The higher the intensity of the radiating source, the greater should be the energy distributed over the wave front.
The first law of photoelectric emission does not imply any deviation from the electromagnetic theory since the magnitude of the photoelectric current is proportional to the incident light intensity.
The surprising thing is that the velocity of the photoelectrons is not raised with an increase in the intensity of the illumination on the surface of an emitter, contrary to what the wave theory suggests. Measurements of emission cutoff potentials over very large ranges of intensities show that the maximum kinetic energy of photoelectrons is independent of the light intensity.
According to the wave theory, light of any frequency should cause photoelectric emission provided it is intense enough. Experiments show, however, that all substances have characteristic cutoff frequencies below which emission does not occur, no matter how intense the illumination.
On the other hand, a very feeble light containing frequencies above the threshold value causes the ejection of photoelectrons.
Again, from the wave theory we could argue that given enough time an electron in an area illuminated by a very feeble light would "soak up" enough energy to escape from the surface.
No such time lag between the illumination of a surface and the ejection of a photoelectron has ever been measured. If emission of photoelectrons occurs at all, it begins simultaneously with the illumination of a photosensitive surface.
The wave theory, which serves so well in the explanation of radiation transmission phenomena, is incapable of describing the processes of radiation absorption observed in the photoelectric effect. In this instance a particle model of light appears to be useful.
Had Newton perhaps been on the right track after all? The classic particles of Newton's theory could explain the relation between photoelectron emission rate and intensity of illumination but not that between photoelectron velocities and frequency of illumination.
The discovery of the photoelectric effect, coming as it did from the experiments that established the correctness of the electromagnetic wave theory, presented a paradox to twentieth century physicists. Was there no theory to explain these widely divergent phenomena?
12.9 The Quantum Theory Aside from the disturbing implications that the photoelectric effect introduced into twentieth century physics, physicists were much concerned about discrepancies between their experimental studies of absorption and emission of radiant energy and the requirements derived from the electromagnetic radiation theory.
The first great step toward the resolution of these discrepancies was taken by the German theoretical physicist Max Planck (1858-1947).
In 1900 Planck was investigating the spectral distribution of electromagnetic radiation from a hot body. Classic electromagnetic theory predicted that the emission intensity would increase continuously as the radiation frequency increased.
The spectral distribution of radiated energy measured experimentally was very different from that predicted by theory at the higher frequencies. It approached zero rather than infinity as the frequency increased without limit.
Clearly something was wrong in this prediction that the radiated energy would keep on increasing with frequency without limit.
Planck found that he could bring radiation theory and experiment into agreement by assuming the energy emitted by the radiating sources to be an integral multiple of a fundamental quantity hf, where h is a universal constant now known as Planck's constant, and f is the frequency of these radiating sources.
To explain why this bold assumption worked, he postulated that light is radiated and absorbed in indivisible packets, or quanta. We now call these packets, or quanta, photons.
The amount of energy comprising a photon is determined by the frequency of the radiation. It is directly proportional to this frequency since
E = hf
When f is given in hertz and h in joule seconds (h = 6.63 x 10-34 j s), the energy E of a photon is expressed in joules.
Planck published his quantum hypothesis in 1901 and, although not immediately accepted, it was destined to profoundly influence the new physics emerging with the twentieth century.
Certainly there is nothing in the classical physics of Newton to suggest that certain values of energy should be allowed and others should not. Albert Einstein recognized the value of Planck's quantum hypothesis in connection with the photoelectric effect.
He reasoned that since emission and absorption of light radiation occurs, discontinuously, certainly the transmission field should be discontinuous.
Proceeding with this hypothesis, in 1905 Einstein published a very simple and straightforward explanation of the photoelectric effect. A few years later, the accurate experimental work off Millikan, Hughes, and Compton established the correctness of Einstein's explanation.
The bold extension of Planck's quantum ideas by Einstein firmly proved the quantum theory, which assumes that the transfer of energy between light radiations and matter occurs in discrete units called quanta, the magnitude of which depends on the frequency of the radiation.
I 12.10 12.10 Einstein's Photoelectric Equation According to Einstein, light illuminating an emitter surface consists of a stream of photons. When a photon is absorbed by the emitter, its quantum of energy hf is transferred to a single electron within the surface. If the acquired energy is sufficient to overcome the surface barrier and the electron is moving in the right direction, the electron will escape from the surface.
In penetrating the surface, the electron must give up a certain energy w, the work function of the substance. If the energy hf imparted by the photon is greater than w, the electron will have kinetic energy as indicated by its velocity after leaving the surface.
The maximum kinetic energy possessed by photoelectrons ejected from an emitter illuminated by light of frequency f was given by Einstein as
1/2mv2max = hf - w
where m and v are the mass and velocity, respectively, of the photoelectrons, h is Planck's constant, f is the frequency of the impinging light radiation (the product hf is the energy of the photon), and w is the work function of the emitting material.
Now, recalling the failures of the wave theory to explain photoelectric emission, we find no such difficulties in the application of Einstein's photon hypothesis. A lower light intensity means fewer photons impinging on the emitter surface in a given period of time and fewer photoelectrons ejected.
However, as long as the frequency of the incident light remains unchanged, each photon transfers the same energy hf to the electron when a collision occurs. Einstein's photoelectric equation shows clearly why light of too low a frequency will not cause photoelectric emission from a given material no matter how intense the illumination.
Photon energy is a linear function of the frequency of the light since it equals the product hf. Now if 1/2mv2fmax = 0, it follows that
hfco = w
Here the photon can impart to the electron just enough energy for it to penetrate the surface barrier. No energy is left over to appear as electron velocity. The frequency in this situation is the cutoff frequency fco Illumination of any lower frequency on this emitter will consist of photons with energy hf < w, and photoelectric emission cannot occur no matter how many photons there are. If photons have enough energy to eject electrons, no "soaking up" time is required before a feeble light can start the photoelectric emission process.
This is true because the ejection energy for each photoelectron is delivered in a single concentrated bundle.
The quantum theory, which provides a particle model of light, meets every objection raised when the electromagnetic wave theory is employed to interpret photoelectric emission phenomena. Yet many experiments have proved the correctness of the wave theory.
When we consider the full range of radiation phenomena, we are persuaded that light must have a dual character. In some circumstances it behaves like waves, and in other circumstances it behaves like particles.
The modern view of the nature of light recognizes this dual character: Radiant energy is transported in photons that are guided along their path by a wave field.
12.12 The Quantized Atom Striking evidence favoring the quantum theory was given by Niels Bohr (1885-1962), who in 1913 devised a model of the atom based on quantum ideas.
Ernest Rutherford (1871-1937), the English physicist, had conducted experiments (described in Section 23.7) that in 1911 led him to postulate the nuclear atom with its planetary arrangement of electrons.
This model of Rutherford's immediately encountered difficulties when subjected to the classical laws of physics, that is, the known laws of mechanics and electromagnetism as formulated by Newton and Maxwell.
The electromagnetic theory predicts that charged particles undergoing acceleration must radiate energy. Indeed, this accounts for the radiation of energy from a radio transmitting antenna.
A planetary electron moving about the nucleus of an atom experiences acceleration and accordingly should radiate energy. As energy is drained from the electron, it should spiral in toward the nucleus causing the atom to collapse. Of course atoms do not collapse, and so this classical model cannot be correct.
Bohr assumed that an electron in an atom can move about the nucleus in certain discrete orbits without radiating energy. Such orbits represent "allowable" energy levels in the Planck concept.
The level closest to the nucleus corresponds to the orbit of lowest energy. This position could account for the stability of an atom. However, atoms do radiate energy. Bohr assumed further that an electron may "jump" from one discrete orbit to another of lower energy.
Ah, the Goose Chart!
In the process a photon is emitted. Its energy represents the difference between the energies of the levels involved in the transition. The frequency of the emission is proportional to this energy difference, the proportionality factor being Planck's constant h. Thus the frequency of the photon emission depends on the magnitude of this energy change
The return of excited atoms to their stable state results in the emission of bright line spectra.
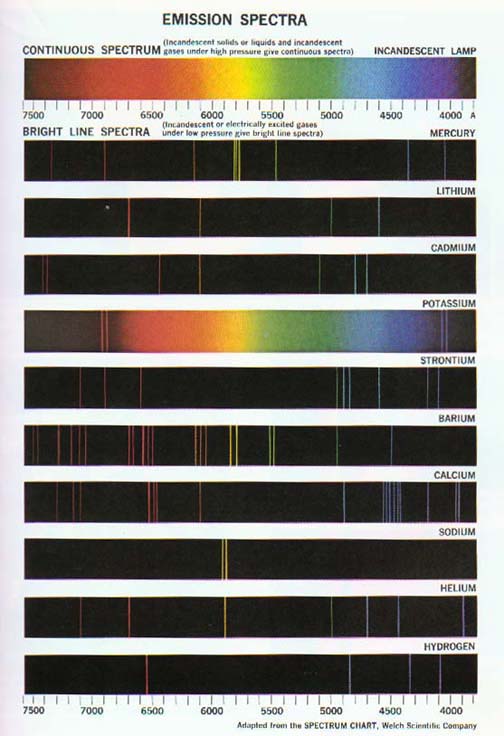
Excited hydrogen atoms produce the simplest such atomic spectra. Hydrogen lines appear in several series in and beyond the visible region of the radiation spectrum. These include the Balmer series in the visible region, the Lyman series in the ultraviolet region, and the Paschen series in the near infrared region. See Figures 12-15 and 12-16.
Numerous attempts had been made to account for the discrete frequencies of the bright lines observed in these spectra. It was Bohr who first associated spectral lines
With pairs of energy levels, thus marking the initial step in the development of the quantum mechanics of atomic structure.
Bohr's atom model provided no information about the mechanics of photon emission when an electron passes from a higher to a lower energy level; but his concept of energy levels provided a great stimulus for theoretical studies in this field.
In 1924 the French physicist Louis de Broglie (b. 1892) suggested that the dual particle and wave nature of light provided evidence of the wave nature of particles as well. Accepting Einstein's idea of the equivalence between mass and energy, he postulated that in every mechanical system, waves are associated with matter particles.
The application of this concept of matter waves to the study of the structure of matter is known as wave mechanics. Just as the ordinary laws of mechanics are essential to any explanation of the behavior of objects of large dimensions, wave mechanics is necessary in dealing with objects that have atomic and subatomic dimensions.
A photon has energy that is the product of Planck's constant and its radiation frequency.
E = hf
In Einstein's equation E = mc2 for mass-energy equivalency, m is the mass of the particle while in motion. When at rest, its mass mo, known as the rest mass, is smaller than m.
If we consider the energy of the photon to be equivalent to that of a moving particle, then
hf = mc2
and we could solve for m. However, this solution would also imply a certain rest mass for the photon. But a photon is never at rest; it always moves with the speed c. Photons do have momentum and can transfer it to any surface on which they impinge. Calculating this momentum mc, we get
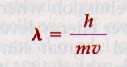
There is abundant evidence today of the wave nature subatomic particles. Accelerated electrons have been found to behave like X rays. The electron microscope is application of electron waves. The development of quantum theory and the system of wave mechanics have provided physicists with their most powerful means of studying the structure and properties of matter. Matter waves will be discussed more extensively in Chapter 25.
12.12 Coherent Light: the Laser Common light sources such as fluorescent and incandescent lamps radiate light in all directions over a wide range of frequencies with random phase relationships.
Even groups of waves of the same frequency have random phase relationships. These disordered light waves are said to be incoherent. A stationary interference pattern is described in Section 10.15 and represented in Figures 10-27 and 10-28.
To produce such a pattern, it is necessary to employ two wave trains with identical wavelengths and a constant phase relationship. Such wave trains have coherence; they are said to be coherent waves.
It is not difficult to obtain coherence from two sources of sound waves. However, a stationary interference pattern from light waves is ordinarily produced in a high school laboratory by means of a subtle arrangement using a single source of incoherent light.
Coherent light is produced by a remarkable instrument called a laser.
It is a light amplifier that functions because of stimulated emissions of radiation. The term "laser' is an acronym derived from the description of its function: Light Amplification by Stimulated Emission of Radiation.
The laser output is a single-frequency (monochromatic) radiation of parallel waves with a constant phase relationship. The first successful laser produced a pulsed coherent red beam from a ruby crystal. The ruby laser was followed by gaseous lasers which produced continuous coherent beams. Today there are many different types of lasers using gases, liquids, crystals, semiconductors, glass, and plastics.
These lasers produce coherent beams of different spectral colors. Laser research is continuing on a broad front. Industry, engineering, medicine, communications, photography, and the military are areas in which lasers are being used. Scientists and engineers are constantly finding new applications.
l2.24 The Pressure of Light The electromagnetic theory of Maxwell predicted that incident light should exert a pressure applied in the direction of the radiation. According to Maxwell, the pressure on a totally reflecting surface should be twice that on a totally absorbing surface illuminated by the same radiation.
In 1901 Nichols and Hull in the United States and Lebedev in Russia succeeded experimentally in measuring pressure of light. Their results were in such close agreement with theory as to provide proof of the existence of light pressure.
What does the particle model tell us about the pressure of light?
Our common experiences with pressure are those involving collisions of particles in motion. Since particle collisions are momentum problems, conservation of momentum applies.
A perfectly elastic ball rebounding from an object transfers twice the momentum that a perfectly inelastic ball having the same mass and velocity would transfer.
When a beam of photons is incident on a totally absorbing surface, the pressure exerted depends on the rate of change of photon momentum per unit area of illuminated surface.
The pressure of light is exceedingly small in comparison to pressures we commonly experience. The pressure of sunlight on the earth is approximately 4 x 10-11 atmosphere.
Comet tails always point away from the sun, apparently due to the pressure of sunlight and solar particles on the extremely diffuse matter in them.
ILLUMINATION
12.15 Luminous and IIIuminated Objects Nearly all the natural light we receive comes from the sun. Distant stars account for an extremely small amount of natural light. Of course, moonlight is sunlight reflected from the surface of the moon.
We produce light from artificial sources in several ways. Materials may be heated until they glow, or become incandescent, as in an electric lamp. Molecules of a gas at reduced pressure may be bombarded with electrons to produce light, as in a neon tube. Most of the visible light from fluorescent tubes results from the action of ultraviolet radiations on phosphors that coat the inside surface of the glass tubes. The firefly produces light by means of complex chemical reactions.
Most artificial sources of light are hot bodies that radiate energy in the infrared region of the spectrum as well as visible light. The energy of the thermal radiation emitted by hot bodies depends upon the temperature of the body and the nature of its surface
At a temperature of 300 oC the most intense radiation emitted by a hot body has a wavelength of about 5 x 10-4 cm, well down in the infrared region of the electromagnetic spectrum.
As the temperature is raised to 800 oC, enough radiation is emitted in the visible region to cause the body to appear "red hot" although the bulk of the energy radiated is still in the infrared region. If the temperature of the body is raised to 3000 oC, the most intense emission remains in the near infrared region, however, there is enough blue visible radiation to cause the body to appear "white hot.". This last temperature is near that of the filament of an incandescent lamp.
Hence such lamps have low efficiencies as producers of visible radiation. Generally the efficiency improves as the filament temperature is raised. The white-hot filament of an incandescent lamp is said to be luminous. It is visible primarily because of the light it emits.
An object that gives off light because of the energy of its accelerated particles is said to be luminous. The sun and the other stars are luminous objects. Just as radiant heat may be reflected, light may be reflected from the surfaces of objects.
Mirrors reflect a beam of light in a definite direction. Other surfaces scatter the light that is incident on them in all directions. An object that is seen because of the light scattered from it is said to be illuminated
The moon is illuminated, for it reflects radiant energy from the sun. Some of the light energy arriving at the surface of an object is reflected, some of it is transmitted, and some of it is absorbed.
Any dark-colored object absorbs light, but a black object absorbs nearly all the light it receives. When the rays of the sun strike a body of water vertically, most of them are either absorbed or transmitted.
Most of the rays are renflcted, however, when they strike the water at an oblique angle. For this reason the image of the sun can be seen in the water without discomfort when the sun is directly overhead, but not when the sun is near the horizon.
Air, glass, and water transmit light readily and are said to be transparent. Other substances transmit light but scatter or diffuse it so that objects seen through them cannot be identified. Such substances are translucent.
Typical examples are frosted electric lamps and parchment lamp shades.
Opaque substances do not transmit light at all. From a luminous point source, light waves travel outward in all directions. If the medium through which they pass is of the same nature throughout, the light progresses along the normal to the wave front. A single line of light from a luminous point is called a ray; a group of closely spaced rays forms a beam of light.
Small beams are referred to as pencils. See Figure 12-19.
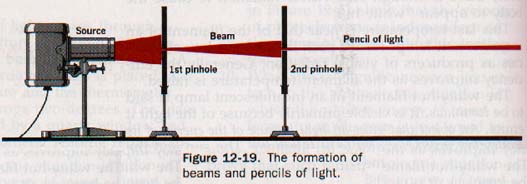
Light coming from the sun is in rays so nearly parallel that it may be considered as a parallel beam. When several rays of light come from a point, they are called a diverging pencil, while rays proceeding toward a point form a converging pencil. When the sun's rays pass through a magnifying glass, they converge at a point called a focus.
Because an opaque object absorbs light, it casts a shadow in the space behind it. When the source of light is a point, as in Figure 12-20(A), an opaque ball, B, cuts off all the rays that strike it and produces a shadow of uniform darkness on the screen, S. If the light comes from an extended source, the shadow varies in intensity, as shown in Figure 12-20(B).
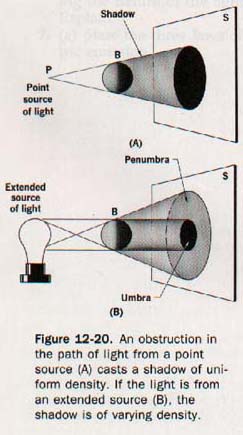
The part from which all the rays of light are excluded is called the umbra; the lighter part of the shadow is the penumbra. Within the region of the penumbra the luminous source is not entirely hidden from an observer. The umbral and penumbral regions of the moon's shadow cast during a solar eclipse are shown in Figure 12-21.

12.16 The Speed of Light The speed of light is one of the most important constants used in physics, and the determination of the speed of light represents one of the most precise measurements ever achieved.
Before 1675 light propagation was generally considered to be instantaneous, although Galileo had suggested that a finite time was required for it to travel through space. In 1675 the Danish astronomer Olaus Roemer (1644-1710) determined the first value for the speed of light.
He had been puzzled by a variation in his calculations of the time of eclipse of one of Jupiter's satellites as seen from different positions of the earth's orbit about the sun. Roemer concluded that the variation was due to differences in the distance that the light traveled to reach the earth.
Very precise modern measurements of the speed of light are made using laboratory methods. The most notable experiments were performed by Albert A. Michelson (1852-1931), a professor of physics at the University of Chicago, who measured the speed of light in air and in a vacuum with extraordinary precision.
1. The speed of light in air. Michelson measured the speed of light over the accurately determined distance between Wilson and Mt. San Antonio, California. His method is illustrated in principle by Figure 12-22. The light source, octagonal mirror, and telescope were located on Mt. Wilson and the concave mirror and plane mirror were located on Mt. San Antonio, 35.4 km away. The octagonal mirror, M, could be rotated rapidly under controlled conditions and was timed very accurately.
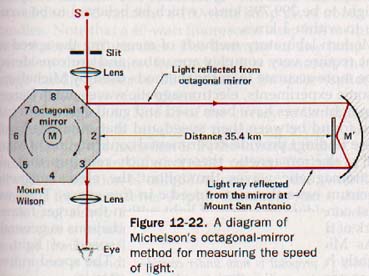
With mirror M stationary, a pencil of light from the slit opening was reflected by M1 to the distant mirror M', from which it was returned to M3 . The image of the slit in the mirror at the M3 poSition could be observed accurately through the telescope.
The octagonal mirror was then set in motion and the speed of rotation brought up to the value that moved M2 into the position formerly occupied by M3 during the time required for the light to travel from M1 to Mt. San Antonio and return. The slit image was again seen in the telescope precisely as it was when the octagon was stationary. The light traveled twice the optical path of 35.4 km in one eighth of the time of one revolution of the octagonal mirror. Thus where MM' is the optical path, t is the time of revolution of the octagon, and c is the speed of light.
Michelson's investigation of the speed of light required several years to complete.
The optical path was measured by the U.S. Coast and Geodetic Survey and found to be 35,385.5 meters, accurate to about one part in seven million.
The rate of the revolving mirror was measured by stroboscopic comparison with an electric signal of standard frequency. The average of a large number of determinations yielded a speed of light in air of 299,729 km/s.
2. The speed of light in a vacuum. Michelson conducted similar experiments using an evacuated tube 1.6 km long to eliminate the problems of haze and variations in air density. In these investigations he determined the speed of light to be 299,796 km/s, which he believed to be accurate to within 1 km/s.
Modern laboratory methods of measuring the speed of light require very complex apparatus and are considered to be more accurate than the methods used by Michelson.
In some experiments, electromagnetic waves much longer than light waves have been used and good agreement has been found between their speed and that of visible light.
These findings provide experimental confirmation of Maxwell's electromagnetic theory, which requires that all electromagnetic waves throughout the electromagnetic spectrum have the same speed c in free space.
Thus we must consider the speed of light within the larger framework of the speed of electromagnetic radiations in general. As Michelson's figures show, the speed of light is slightly higher in a vacuum than in air. The speed in free space generally accepted as most accurate is 2.99792458 x 108 m/s with an uncertainty of 1.2 m/s. Physicists now conduct laser experiments in their quest for improved accuracy in the determination of this important constant.
c = 2.99792458 x 108 m/s
12.17 Light Measurements The quantitative study of light is called photometry. Three quantities are generally measured in practical photometry: the luminous intensity of the source; the luminous flux, or light flow, from a source; and the illumination on a surface.
1. Luminous intensity. In order to derive a set of photometric units it is necessary to introduce an additional fundamental unit into our measurement system. The unit for luminous intensity, I, is the arbitrary choice. It is the candle, cd.
The candle is known internationally as candela. Originally the light from a certain type of candle was used as a standard, but this has been replaced by a more readily reproducible source of luminous intensity.
The candle is one sixtieth of the luminous intensity o a square centimeter of a black-body radiator maintained at the temperature of freezing platinum (2046 oK).
In practice it is convenient to use incandescent lamps that have been rated by comparison with the standard.
Incandescent lamps used for interior lighting generally have an intensity ranging from a few candles to several hundred candles. The common 40-watt lamp has an intensity of about 35 candles; a 100-watt lamp gives about 130 candles. Note that a 40-watt fluorescent lamp has an intensity of about 200 candles. The intensity of any lamp depends on the direction from which it is measured; the average candle power in all directions in space (spherical candle power) is often given.
2. Luminous flux. Not all of the energy radiated from a luminous source is capable of producing a visual sensation. Most of the radiation is in the infrared region, and a small amount is in the ultraviolet region.
The rate of flow of visible radiation is called luminous flux, the symbol for which is the Greek letter phi. Luminous flux is that part of the total energy radiated per unit of time from a luminous source that is capable of producing the sensation of sight. The unit of luminous flux is the lumen, Lm.
Suppose a standard light source of 1 candle is placed at the center of a hollow sphere having a radius of 1 meter, as illustrated in Figure 12-24.
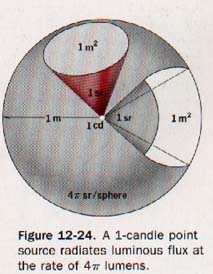
The luminous source is presumed to radiate light equally in all directions and to have such small dimensions that it may be termed a "point source."
The area of the surface of a sphere of radius r is equal to 4π2. Since the radius of the unit sphere is 1 meter, its surface area is 4π x (1 m)2.
One lumen of flux is radiated by the 1-candle source to each square meter of inside surface of the sphere. The lumen is the luminous flux on a unit surface all points of which are at unit distance from a point source of one candle.
3. Illumination. In Figure 12-24 it is evident that as the intensity of the source is increased, the luminous flux transmitted to each unit area of surface and the flux of each unit area are similarly increased.
The illumination of the surface is said to be increased. Illumination is the density of the luminous flux on a surface. When the surface is uniformly illuminated, the illumination is the quotient of the flux on the surface divided by the area of the surface and is expressed as the luminous flux per unit area.
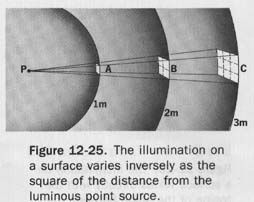
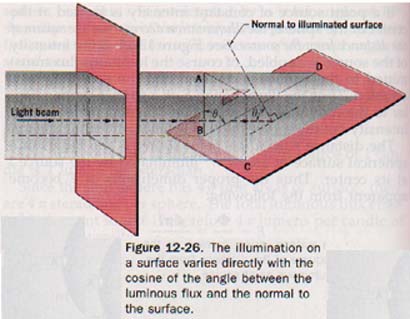
The illumination on a surface varies inversely with the square of the distance from the luminous source and directly with the cosine of the angle between the luminous flux and the normal to the surface.
This explains the seasons of the year. The angle of attack determines how much solar radiation is present.
The Bunsen photometer is used to measure illumination. When the illumination is the same on each side,
E1 = E2
so
I1/r12 = I2/r22
SUMMARY
A particle model and a wave model were developed in the seventeenth century to explain the then known properties of light. The particle model failed after additional properties of light were discovered.
The wave model prevailed, and with the experimental confirmation of the electromagnetic theory the wave model of light was thought to be complete.
The discovery of the photoelectric effect, the failure of the electromagnetic theory, and the success of the quantum theory in explaining photoemission established the dual character of light. placed so that both sides are equally illuminated?
An object is luminous if it is visible because of the light it emits.
An object is illuminated if it is visible because of the light it reflects. An object may reflect, absorb, or transmit the light it receives.
Opaque objects cast shadows when illuminated. Shadows may consist of umbras and penumbras.
Photometry is the quantitative study of light. Three quantities measured in practical photometry are luminous intensity, luminous flux, and illumination. The intensity of a light source can be measured by means of a photometer.
VOCABULARY
coherent light, converging pencil, corpuscular theory, diverging pencil, electromagnetic spectrum, electromagnetic wave, Huygens' principle, illuminated object, illumination, incoherent light, inverse square law, laser, lumen, luminous flux, luminous object, penumbra, photoelectric effect, photoelectron, photometer, photometry, Planck's constant, radiant energy, rectilinear propagation, Snell's law, umbra, visible spectrum.
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester