Sound Waves

Sound Waves

The purpose of this is to give quick reference to information or to use in an emergency (like if your text has accidentally been left under your desk at school).
This is NOT intended to replace reading the text with its excellent photographs, diagrams, charts, and tables.
SOUND WAVES
I1.1 The Sonic Spectrum The energy-transfer mechanism of compression waves is a major interest of physicists. In a medium having elastic and inertial properties, compression waves propagate as longitudinal disturbances.
The disturbances consist of compressions and rarefactions that give rise to elastic forces in the propagating (transmitting) medium. Through these elastic forces the energy of the wave is transferred to the particles of the medium that are next in line.

The energy exchange is continuous as particles receive wave energy and pass it along. The frequency range over which such longitudinal waves occur is very large. It is called the sonic spectrum.
There is no clearly defined lower limit of frequency of the sonic spectrum. However, the frequency of an earthquake wave may be a fraction of a cycle per minute and its wavelength may be measured in kilometers.
The upper limit of the sonic spectrum is well defined. For a constant-velocity condition, periodic waves of increasing frequency have proportionally decreasing wavelength. A wave is not transported by a medium in which the wavelength is small compared to the inter-particle spacing of the medium.
For a gas the mean free path of the molecules is the limiting dimension. Thus at ordinary temperatures and pressures the upper range of sonic frequencies is of the order of 109 hertz in a gaseous medium. In liquids and solids the upper frequency limit is higher because of the smaller inter-particle spacing.
Within the sonic spectrum lies the region of sound, a range of compression-wave frequencies to which the human ear is sensitive. This audible range of frequencies, called the audio range, or the audio spectrum, extends from approximately 20 to 20,000 hertz.
Compression waves at frequencies above the audio range are referred to as ultrasonic; those below the audio range are referred to as infrasonic.
11.2 The Production of Sound A sound is produced by the initiation of a succession of compressive and rarefactions disturbances in a medium capable of transmitting these vibrational disturbances.
Particles of the medium acquire energy from the vibrating source and enter the vibrational mode themselves. The wave energy is passed along to adjacent particles as the periodic waves travel through the medium.
Such vibrating elements as reeds (clarinet, gooseophone), strings (guitar, vocal cords), membranes (drum, loudspeaker), and air columns (pipe organ, flute) initiate sound waves.
Sound waves are transmitted outward from their source by the surrounding air. When they enter the ear, they produce the sensation of sound.
Suppose we clamp one end of a thin strip of steel in a vise to serve as a vibrating reed. When struck sharply, the free end vibrates to and fro. See Figure 11-2.
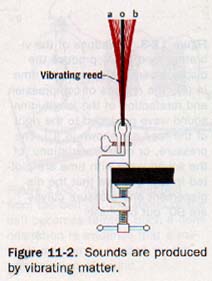
If the reed vibrates rapidly enough, it produces a humming sound. When the reed vibrates, its motion approximates simple harmonic motion. See Figure 11-3(A).
A graph of its displacement with time produces the sine wave shown in Figure 11-3(B).
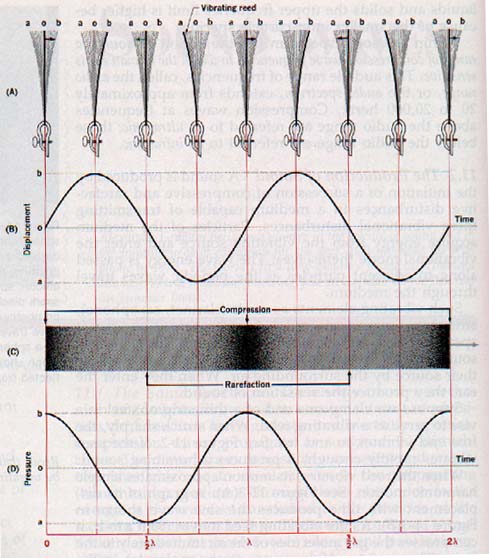
As the vibrating reed moves from a to b, it compresses the gas molecules of the air immediately to the right.
The reed transfers energy to the molecules in the direction in which the compression occurs. At the same time the air molecules to the left expand into the space behind the moving reed and become rarefied. Thus the movement of the reed from a to b produces a compression and rarefaction simultaneously with a net transfer of energy to the right, the direction of the compression.
As the reed moves in the reverse direction from b to a, it compresses the gas molecules to the left, while those to the right become rarefied.
The combined effect of this simultaneous compression and rarefaction transfers energy to the left, again in the direction of the compression. If we consider just the series of compressions and rarefactions produced to the right, it is apparent that the maximum compression occurs as the reed moves through its equilibrium position o traveling from a to b. See Figure 11-3(C).
The maximum rarefaction occurs as the reed moves through its equilibrium position o traveling from b to a. This is shown in (D) as a plot of the variation of pressure with time.
Simultaneously, of course, a corresponding series of rarefactions and compressions is produced to the left. The vibration of the reed thus generates longitudinal trains of waves. In these longitudinal waves, vibrating gas molecules move back and forth along the path of the traveling waves, receiving energy from adjacent molecules nearer the source and passing it on to adjacent molecules farther from the source. Sound waves are longitudinal waves.
1.3 Sound Transmission To produce sound waves, we must have a source that initiates a mechanical disturbance and an elastic medium through which the disturbance can be transmitted.
Most sounds come to us through the air, and it is the air that acts as the transmitting medium. At low altitudes, we usually have little difficulty hearing sounds. At higher altitudes, where the density of the air is lower, less energy may be transferred from the source to the air. Dense air is a more efficient transmitter of sound than rarefied air.
The following experiment provides evidence that a material is required for the transmission of sound. An electric bell under a bell jar is connected to a source of energy so that it rings.

While it is ringing, air is removed from the bell jar. As the remaining air becomes less and less dense, the sound becomes fainter and fainter. When air is allowed to reenter, the sound becomes louder.
These effects show that it is increasingly difficult to effect the transfer of sound energy to the air as the density of the air decreases. This demonstration suggests that if all the air could be removed from the bell jar, no sound would be heard. Sound does not travel through a vacuum; it is transmitted only through a material medium.
The sound of two rocks being struck together under water can be heard quite plainly by a swimmer submerged in the water. If the swimmer is near the source of the disturbance, the effect can be painful. Liquids are efficient transmitters of sound.
11.4 The Speed of Sound During a thunderstorm, a distant lightning flash can be seen several seconds before the accompanying thunder is heard. The timer at the finish, line during a track meet may see the smoke from the starter's gun before she hears the report. Over short distances, light travels practically instantaneously.
Therefore, the; time that elapses between a lightning flash being seen and the thunder being heard or between a gun being fired and the report being heard must be the time required for the sound to travel from its source to the listener.
The speed of sound in air is 331.5 m/s at OoC. This speed increases with temperature about (0.6 m/s)/Co.
The speed of sound in water is about four times the speed in air. In water at 25oC sound travels about 1500 m/s. In some solids, the speed of sound is even greater. In a steel rod, for example, sound travels approximately 5000 m/s-- about 15 times the speed in air.
In general the speed of sound varies with the temperature of the transmitting medium. For gases the change in speed is rather large. For liquids and solids, however, this change in speed is small and is usually neglected. Representative values for the speed of sound waves in various media are given in Table 11-1. (See also Appendix B, Table 17.)

12.5 The Properties of Sound A nearby clap of thunder is loud; a whisper is soft. A cricket has a shrill, high chirp; a bulldog has a deep growl. A violin string bowed by a virtuoso produces a note of fine quality and is far more pleasing to hear than that produced by the novice.
Each of these sounds has characteristics clearly associated with it. Sounds differ from each other in several fundamental ways. We shall consider three physical properties of sound waves: intensity, frequency, and harmonic content. The effects of these properties on the ear are called, respectively, loudness, pitch, and quality.
11.6 Intensity and Loudness The intensity of a sound is the time rate at which the sound energy flows through a unit area normal to the direction of propagation. Intensity thus has the dimension of power/area.
I = P/A
Where P is sound power in watts and A is area in square centimeters, the sound intensity I is expressed in watts per square centimeter.
The intensity of a sound wave of given frequency is dependent on its amplitude; it is proportional to the square of the amplitude.
Sound waves that emanate from a vibrator approximating a point source and that travel in a uniform medium spread out in a spherical pattern. Thus the area of the expanding wave front is directly proportional to the square of its distance from the source.
Since the total power of the wave is constant, the intensity of the wave diminishes as it moves away from the source. The sound produced by a whistle is only one-fourth as intense at a distance of one kilometer as it is at a distance of half a kilometer from the source.
The intensity of sound in a uniform medium is inversely proportional to the square of its distance from the point source.
The loudness of a sound depends on an auditory sensation in the consciousness of a human listener. In general, sound waves of higher intensity are louder, but the ear is not equally sensitive to sounds of all frequencies. Thus a high or a low-frequency sound may not seem as loud as one of mid-range frequency having the same intensity.
An increase in the intensity of a sound of fixed frequency causes it to seem louder to the listener. Suppose a 1000-hz tone is generated of such low intensity that it is barely audible. The intensity can be increased approximately 1012 times before the tone becomes so loud that it is painful to the listener.
While the intensity of a sound can be directly measured with instruments, the loudness can not as it depends on the ear and subjective judgment of the listener.
11.7 Relative Intensity Measurements Intensity is measured with acoustical instruments and does not depend on the hearing of a listener. At 1000 hz the intensity of the average faintest audible sound, called the threshold of hearing, is 10-16 w/cm2.
When expressing the intensity of a sound, it is often compared with the intensity of the threshold of hearing and this ratio of intensities yields an expression of the relative intensity of the sound. Because of the great range of intensities over which the ear is sensitive, a logarithmic rather than an arithmetic intensity scale is used. The unit of relative intensity is the decibel (db). Here are some common examples:

11.8 Frequency and Pitch Pitch is the characteristic of a sound that depends on the frequency the ear receives. It is the pitch that allows us to assign the sound its place in the musical scale.
We usually distinguish between a musical tone and a noise by the fact that the former is a pleasing sound, the latter is a disagreeable one.
Tone is associated with the pleasing quality of sound the that reaches the ear. Tone quality is enhanced by the complexity of the sound wave that reaches the ear, that is, by the number and distribution of harmonics of the fundamental frequency superposed in the complex sound wave.
Pitch is principally with the fundamental frequency of the complex sound wave. This distinction is important when considering the quality of musical sounds. For example, notes the same pitch sounded by the oboe and the violin are very different in tonal quality.
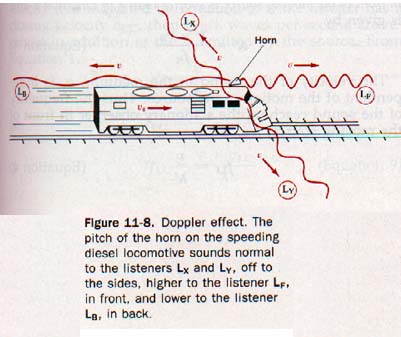
11.9 The Doppler Effect In our discussion of frequency and pitch in Section 11.8, both the source of the emission and the listener were assumed to be stationary. In that case the pitch of the sound heard is characteristic of the frequency of the emission.
If the source emits 1000 vibrations per second, the listener hears a 1000-hz tone. When there is relative motion between the source of sound and the listener, the pitch of the sound heard is not same as that when both listener and source are stationary. Two situations are common: The source may be moving the listener is stationary, and the listener may be moving and the source is at rest.
The first situation prevails when the listener stands at a crossing while a train passes. The pitch of the horn of the locomotive drops abruptly as the passes the listener's position.
The second situation occurs when the listener rides in the train as it passes a highway intersection. In this instance the pitch the warning bell at the crossing drops abruptly as the train passes through the intersection.
In both situations the steady pitch of the sound heard by observer is higher than the actual frequency of the source would indicate as the distance between the listener the source decreases at a constant rate.
Also, the steady pitch of the sound heard is lower than the actual frequency the source would indicate as the distance between the listener and the source increases at a constant rate.
The change in pitch produced by the relative motion of the source and observer is known as the Doppler Effect. Of course, the frequency of the sound emitted by the source remains unchanged as does the velocity of the sound in the transmitting medium. Figure 11-8 illustrates this principle.
The Formulae for the Doppler Effect:


Where fL is the frequency heard by the listener, fs is the frequency of the source, v is the velocity of the listener, and vs is the velocity of the source.
Remember to get wavelenght, λ, (lambda) use the formula:
![]()

CHARACTERISTIC S OF SOUND WAVES
11.10 Fundamental Tones Suppose a piano wire is stretched about a meter in length between two clamps and drawn tight enough to vibrate when plucked. If plucked in the middle, the wire vibrates as a whole, as shown in Figure I1-11(A).
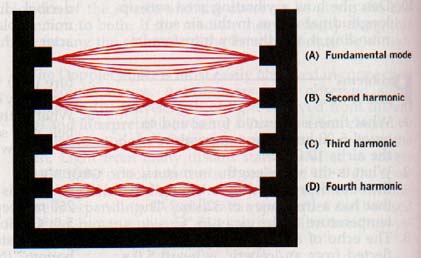
A taut wire or string that vibrates as a single unit produces its lowest frequency, called its fundamental.
A vibrating string, having a small surface area, cuts through the air without disturbing it effectively. The string itself transfers very little of its vibrational energy to the air and therefore produces only a feeble sound. If, however, its vibrations are transferred to a larger surface, such as a sounding board, the air will be disturbed more effectively and a louder sound will be produced.
The sounding board enables a substantial quantity of the vibrational energy to be transferred to the air. In this sense, the sounding board can be thought of as an impedance transformer (Section 10.11), which reduces the impedance discontinuity between the vibrational source and the air. These considerations are enlarged upon in Section 11.14.
The properties of vibrating strings and the sounds they produce can be studied using an instrument called a sonometer. The sonometer may have two or more wires or strings stretched over a sounding board, which reinforces the sound produced by the wires.
Because wires may vary in diameter, tension, length, and composition, a sonometer is useful for studying the effects of these variables on the vibrational characteristics of the wires.
By plucking a string, energy is transferred to the string and causes it to vibrate in transverse wave motion. Just as a vibrating reed transfers energy to molecules of air gases and causes them to exhibit longitudinal wave motion, so a vibrating string transfers energy to these gas molecules and causes them to vibrate and transmit a longitudinal wave.
The frequency of the longitudinal vibration of the molecules, which is the frequency of the sound wave, is the same as the frequency of the transverse vibration of the string. Since the production of sound by a vibrating string dissipates energy, energy must be continuously supplied to the string by plucking or bowing to maintain the sound.
11.11 Harmonics A string may vibrate as an entire unit and may also vibrate in two, three, four, or more segments depending on the standing wave pattern that is on the string. See Figure 11-11(B-D).
When a string is plucked or bowed, not only the fundamental mode but other, higher modes of vibration may be present. Suppose a string vibrates in two segments with a node in the middle, as in Figure Il-11(B).
Its vibrating frequency is twice that of the string vibrating as a single segment. Doubling the frequency of a sound wave raises the pitch one octave. When the string vibrates in four segments, its vibrating frequency (and that of the sound waves produced) is four times its fundamental frequency.
The pitch of the sound produced is then two octaves above the fundamental. The fundamental and the vibrational modes having frequencies that are whole-number multiples of the fundamental are called harmonics.
Only these frequencies can be produced by plucking or bowing the string. By this definition the fundamental is the first harmonic because it is one times the fundamental. The vibrational mode having a frequency twice that of the fundamental is the second harmonic. The vibrational mode of three times that of the fundamental is the third and so on.
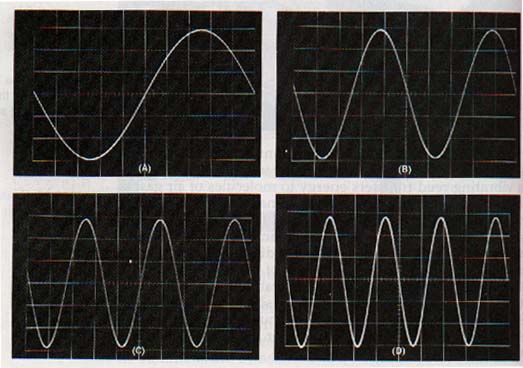
11.12 The Quality of Sound It is not difficult to pick out the sounds produced by different instruments in an orchestra, even though they may be producing the same tone with equal intensity. The difference is a property of sound called quality, or timbre.
If the string of a sonometer is touched very lightly in the middle while being bowed near one end, it will vibrate in two segments and as a whole at the same time, as Figure 11-14 illustrates.

The fundamental is audible, but added to it is the sound of the second harmonic. The combination is richer and fuller; the quality of the sound is improved by the addition of the second harmonic to the fundamental. See Figure 11-15(A).
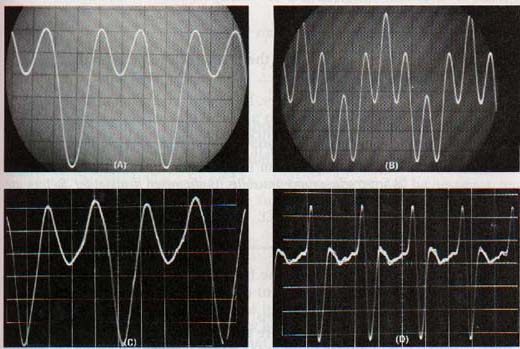
The quality of a sound depends on the number of harmonics produced and their relative intensities. When stringed instruments are played, they are bowed, plucked, or struck near one end to enhance the production of harmonics that blend with the fundamental and give a richer sound. See Figure 11-15(B).
The quality of the tones produced by orchestral instruments varies greatly. For example, the tone produced by a French horn consists almost entirely of the fundamental and the second harmonic. This harmonic content can be recognized by comparing Figures 11-15(A) and ll-15(C). The tonal quality of the trumpet is due to the intensity of its high-frequency harmonics. See Figure ll-15(D).
1.13 The Laws of Strings The frequency of a string is determined by its length, diameter, tension, density.
The strings of a piano produce tones with a range of frequencies. If we examine them we find that strings that produce low-frequency tones are long, and loose, while the strings that produce high tones are short, thin, and taut.
One string produces a tone loud enough for the low-pitched notes, but three are needed to produce high-pitched notes of loudness .
The conditions affecting the frequency of strings are summarized in four laws of strings.
1. Law of lengths. A musician may raise the pitch produced by a stringed instrument by shortening the vibrating length of the string. A violinist shortens the length the A string about 2.5 cm to produce the note B. The frequency of a string is inversely proportional to its length if all other factors are constant.
2. Law of diameters. In a piano and other stringed instruments like the cello and the guitar, the strings that produce higher frequencies have smaller diameters. A string with a diameter of 0.1 cm has twice the frequency of a similar string 0.2 cm in diameter. The frequency of a string is inversely proportional to its diameter if all other factors are constant.
3. Law of tensions. When stringed instruments are tuned, the strings are tightened to increase their frequency or loosened to decrease it. The frequency of a string is directly proportional to the square root of the tension on the string if all other factors are constant
4. Law of densities. The more dense a string is, the lower frequency. Usually three of the strings on a violin are of gut; the fourth is wound with fine wire to increase its so that it can produce the low-frequency tones. The frequency of a string is inversely proportional to the square root of its density if all other factors are constant.

11.1 Forced Vibrations When a tuning fork is struck with a rubber hammer, it vibrates at its fundamental frequency together with some low-order harmonics. The fundamental has a natural frequency that depends upon the fork's length, thickness, and composition. When a key on a piano is struck, the piano string vibrates at its fundamental frequency and at harmonics of this frequency. The only forces that affect these natural rates of vibration are friction and gravitation.
Suppose we strike a tuning fork and then press its stem a table top. The tone becomes louder when the fork is in contact with the table because the fork forces the table top to vibrate with the same frequency. Since table top has a much larger vibrating area than the fork, these forced vibrations produce a more intense sound.
A vibrating violin string stretched tightly between two clamps does not produce a very intense sound. When the string is stretched across the bridge of a violin, however, the wood of the violin is forced to vibrate in response to the vibrations of the string; the intensity of the sound is increased by these forced vibrations. The sounding board of a piano acts in the same way to intensify the sounds produced by the vibrations of its strings.
11.15 Resonance The two tuning forks in Figure 11-17 have the same frequency. They are mounted on sounding boxes that increase the intensity of the sound through forced vibrations. One end of each sounding box is open.
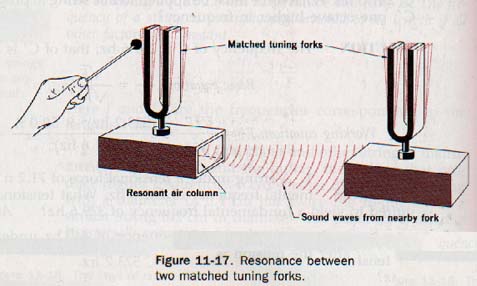
Suppose we place these forks a short distance apart, with the open ends of the boxes toward each other. Now let us strike one fork and, after it has vibrated several seconds, touch its prongs to stop them.
We find that the other fork is vibrating weakly. The compressions and rarefactions produced in the air by the first tuning fork act on the second fork in a regular fashion, causing it to vibrate.
Such action is called resonance, or sympathetic vibration. A person who screams into a piano with the damper pedal depressed may cause the piano strings that produce similar frequencies to vibrate. Fun!
Resonance occurs when the natural vibration rates of two objects are the same or when the vibration rate of one of them is equal to one of the harmonics of the other. If we changed the frequency of one of the tuning forks by adding mass to one of its prongs, we would alter the conditions of the experiment, and no resonance would be evident. Both forks should have the same natural frequency to produce this resonant effect.
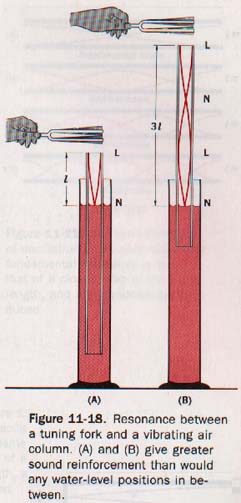
Figure 11-18 illustrates a method of producing resonance between a tuning fork and a column of air. The vibrating fork is held above the hollow cylinder immersed in water. The length of the air column is gradually increased by raising the cylinder.
As seen in Figure 11-18(A), there is a marked increase in the loudness of the sound. Here the column of air in the tube vibrates vigorously at the frequency of the tuning fork, and the two are in resonance. This behavior is similar to the production of a standing wave on a stretched string.
Note: The diagram shows transverse waves because they are easily drawn and analyzed. The actual sound waves are composed of the compressions and rarefactions of a longitudinal wave.
During resonance, a compression of the reflected wave unites with a compression of the direct wave, and a rarefaction of the reflected wave unites with a rarefaction of the direct wave. The constructive superposition of the two waves in phase amplifies the sound.
The resonant air column is simply a standing longitudinal wave system. The water surface in Figure 11-18(A) closes the lower end of the tube and prevents longitudinal displacement of the molecules of the air immediately adjacent to it.
This termination effectively clamps the air column at the closed end and gives rise to a displacement node. Because the upper end of the tube is open, it provides a free-ended termination for the air column and gives rise to a displacement antinode, or loop.
These are, respectively, shown in Figure 11-18(A) as N and L. Because the air particles at the closed end of the tube are unable to undergo longitudinal displacement, they experience maximum changes in pressure.
This position of a displacement node is also a pressure antinode, or a point of maximum pressure change. (Refer to Figure 11-3 for the phase relationship between displacement and pressure waves.) Compressions are reflected as compressions, and rarefactions are reflected as rarefactions. This behavior amounts to a change in phase upon reflection from a rigid termination in the sense that the displacement vector of the air particles is inverted.
The open end of the tube is a displacement loop and, consequently, a pressure node. Here the pressure remains at the constant value of the outside atmosphere, and air rushes into and out of the tube as the column vibrates. It is this large movement of air at the open end of the tube that transfers energy to the atmosphere and provides the reinforcement of the sound produced by the tuning fork.
The fundamental frequency of the resonant column corresponds approximately to a displacement node at the closed end and an adjacent displacement loop at the open end, as shown in Figure ll-18(A). Since the distance separating a node and an adjacent loop of a standing wave is one-fourth wavelength, the length of the closed tube is approximately one fourth the wavelength of its fundamental resonant frequency.
By applying a small empirical correction proportional to the diameter of the tube (because the motion of molecules of the air at the open end of the tube is not strictly in one dimension), we can state the relationship more precisely as follows:
The formulas for close tube and open tube resonators
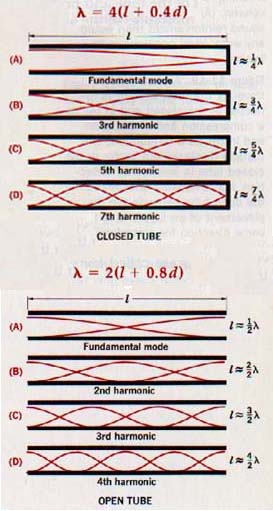
Figures 11-20 & 11-21
From the above discussion we have shown that the normal modes of oscillation of air columns are characterized by
1. a displacement node (or pressure loop) af a closed end, and
2. a displacement loop (or pressure node) at an open end.
Compressions traveling in an open tube are reflected at the open ends as rarefactions, and rarefactions are reflected as compressions. In such reflections, the longitudinal.
11.16 Beats We have already discussed interference of transverse waves in strings and of water waves in the ripple tank in Chapter 10. We were concerned with standing waves in resonant air columns in the preceding section. There is abundant experimental evidence that two or more wave disturbances can travel through the same medium independently of one another.
The superposition principle shows us that the displacement of a particle of a medium at any time is the vector sum of the displacements it would experience from the individual waves acting alone. A standing wave is formed by two wave trains of the same frequency and amplitude traveling through a medium in opposite directions.
We are generally concerned with the conditions or behavior of the space in which the standing wave exists. This generalization is true for resonant air columns used in musical instruments. The standing wave is characterized by an amplitude that varies with distance or position in space.
Two wave trains of slightly different frequencies traveling in the same direction through a medium will interfere in a different way. At any fixed point in the medium through which the waves pass, their superposition gives a wave characterized by an amplitude that varies with time. In Figure 11-22 the resultant displacement of two wave trains of slightly different frequencies is plotted as a function of time.
In curve (A) the frequency is 8 hz, and in (B) it is 10 hz. Curve (C) shows the combined effect of these two waves at a fixed point in their pathway. This resultant wave varies periodically in amplitude with time. Such amplitude pulsations are called beats.
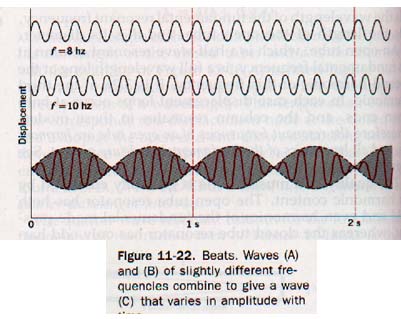
Observe that waves (A) and (B) come into phase two times each second and out of phase the same number of times each second. The beat frequency can be described as two beats per second.
The number of beats per second equals the difference between the frequencies of the component waves.
When the interfering frequencies are audible sounds, the amplitude variations, or beats, are recognized as variations in loudness. The average human ear can distinguish beats up to a frequency of approximately ten per second. The beat phenomenon is frequently used to tune vibrating systems with great precision.
Two vibrating strings can be tuned to the same frequency by adjusting the tension of one until the beats disappear. This tuning procedure is called "zero beating." The piano tuner adjusts frequencies precisely by systematically beating harmonics of notes against each other.
To find the average frequency:
fav = 1/2(fl + fh)
Where fav is the average frequency, fl is the lower frequency, and fh is the higher frequency.
SUMMARY
Sound is a longitudinal disturbance consisting of a succession of compressions and rarefactions to which the ear is sensitive. The term also applies to similar disturbances above and below the normal range of hearing.
A medium having elastic and inertial properties is required for its propagation.
The intensity of a sound is the rate at which the wave energy flows through a unit area. The sensory response to sound intensity is loudness, the sensory response to frequency is Pitch, and the sensory response to harmonic content is tonal quality.
The sensory response to sounds is nonlinear. Minimum intensity levels for hearing various sound frequencies define the threshold of hearing. Upper intensities that produce pain rather than increased loudness define a threshold of pain.
The change in pitch heard when there is relative motion between an observer and a constant-frequency source is called the Doppler effect.
When set in motion, sound generators such as taut strings and air columns vibrate at their fundamental and various harmonic frequencies. The greater the harmonic content of a sound produced by a musical instrument, the higher is its quality and the more pleasing is the auditory response.
The frequency of a vibrating string is determined by its length, diameter, tension, and density.
The laws of strings enunciate the relationships between frequency and these physical factors.
The intensity of a sound generated by a vibrating source can be increased by a sounding board forced to vibrate at the sound frequency.
When forced vibrations are at the natural frequency of the reinforcing body (resonance), maximum reinforcement occurs.
Resonant air columns in the form of open and closed tubes are standing longitudinal wave systems. The resonant length of a closed tube is approximately one-fourth the wavelength of its fundamental frequency, and it resonates at odd harmonics of the fundamental mode.
The resonant length of an open tube is approximately one-half the wavelength of its fundamental frequency, and it resonates at all harmonics of the fundamental mode.
Two wave trains of slightly different frequencies traveling in the same direction in a medium interfere in a way characterized by an amplitude that varies with time at any fixed point in the medium. The amplitude pulsations are called beats. The number of beats per second is the difference between the frequencies of the interfering waves.
VOCABULARY
audio spectrum, beat frequency, beats, compression, decibel Doppler effect, forced vibration, frequency, fundamental, harmonic, infrasonic, intensity, loudness, pitch, propagation, quality, rarefaction, resonance, resonant frequency, sonic spectrum, threshold of hearing, threshold of pain, ultrasonic.
Ah Yaz Indeed!
 Assignment Sheet for this Research Text Only.
Assignment Sheet for this Research Text Only.
 Go to Textbook Assignments for Portfolio:
Go to Textbook Assignments for Portfolio:
.................................First Semester
.................................Second Semester